Volume 6, Issue 4 (Summer 2021)
Health in Emergencies and Disasters Quarterly 2021, 6(4): 235-244 |
Back to browse issues page
Download citation:
BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:



BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:
Mahmoudi H, Pishvaei M S, Saberian P, Slogan M. Presenting A Multi-objective Location Model in GIS Environment: A Case Study in East Tehran Emergency Stations. Health in Emergencies and Disasters Quarterly 2021; 6 (4) :235-244
URL: http://hdq.uswr.ac.ir/article-1-357-en.html
URL: http://hdq.uswr.ac.ir/article-1-357-en.html
1- Department of Industrial Management, North Tehran Branch, Islamic Azad University, Tehran, Iran.
2- Department of Industrial Engineering, Iran University of Science and Technology, Tehran, Iran. ,pishvaee@iust.ac.ir
3- Department of Anesthesiology and Pain, Imam Khomeini Hospital Complex, Tehran University of Medical Sciences, Tehran, Iran.
2- Department of Industrial Engineering, Iran University of Science and Technology, Tehran, Iran. ,
3- Department of Anesthesiology and Pain, Imam Khomeini Hospital Complex, Tehran University of Medical Sciences, Tehran, Iran.
Full-Text [PDF 2652 kb]
(1501 Downloads)
| Abstract (HTML) (4100 Views)
Full-Text: (1023 Views)
1. Introduction
n today’s troubled world, where humanity faces different dangers, an accurate response system with the correct efficiency of prehospital medical emergencies is paramount. An essential feature of emergency service providers worldwide is the rapid deployment of ambulances for patients to save them. Because of the importance of saving human lives and reducing the errors caused by not sending ambulances in time and controlling the death rate, these systems should perform with high precision [1, 2].
The Emergency Medical Service (EMS) is a vital part of any health system. These services operate at a critical point in community health. In most emergencies, there is a very short golden time to provide resuscitation services, which can significantly impact disease or accident prognosis [3]. Success in the EMS system depends on the performance and skills of personnel, their knowledge, best equipment, and facilities. Because of the difficult situation of operation in EMS and the process of much information in a short time, proper decisions should be made as quickly as possible. The sooner the answer is found, the better the results for the patient [4]. Considering the high demand for these services in the east of Tehran City, Iran, and the insufficient EMS bases, the purpose of this study is to find the best places to establish emergency facilities to respond appropriately to all the requests.
Indicators of location-routing problems were determined according to “location of ambulance bases based on random demand”, “optimization of location models”, and “planning and optimization strategies” [7, 6, 5]. In this paper, all research-inspired sub-indices, a part of the sub-indices of the vehicle routing problem, were categorized into two parts: physical and structural sub-indices. In physical sub-indices, only a new constraint is added to the model affected by conditions, such as the type of transport fleet. In structural sub-indices, the set coverage model [8] or more complex possible models are considered, such as the location problem with the maximum expected coverage [9].
One of these efficient models is the Double Standard Model (DSM), used to optimize and improve the location of ambulance services in Belgium [10], Canada [11], and Austria [12]. It is one of the accepted models for related issues is locating an ambulance [13].
To provide comprehensive coverage, using reliability, proposed a distribution algorithm to reduce the number of ambulances at each base implemented and solved the DSM at different periods [14, 15, 16, 17] (Figure 1). They also modeled and solved the ambulance location problem along with the dispatch problem. In this case, the problem with the location and status of each ambulance and all emergency contacts received up to time t were defined [18]. By explaining the prioritization of location indicators, the proposed algorithm optimizes the mathematical model and determines the number and location of ambulances with the assumptions made [19].
By emphasizing the quality of services of emergency stations in New Delhi, using the statistical data of mortality during three years, and collecting data of places prone to demand, the researchers calculated and studied travel time between ambulances to the demand points [20]. In addition, the key indicators in the development of the ambulance airbase were also examined, which had the greatest impact on the distance factor [21].
Based on the research in this field and the study of location indicators in reducing mortality and growth of equitable access to health services in the reviewed articles and also the importance of health development, which is one of the indicators of country development, the primary purpose of the study is to provide an optimal plan to establish emergency stations. This plan consequently improves emergency medical services and reduces the burden of mortality, as well as shortens the response time to accidents.
2. Materials and Methods
One of the main issues for EMS is the correct location of the emergency base and the deployment of the ambulance [9]. Therefore, ambulances must be present at a particular time and distance to the requested location [10], and EMS planners should choose the best sites for establishing and deploying ambulances [11]. Researchers have found that significant deviations from these standards can worsen patients’ conditions [12]. The present study is an applied-developmental study and has used cross-sectional data of the Emergency Organization in East Tehran in 2018. A mixed-integer linear programming model was used to model the problem of optimizing emergency bases.
Integer linear programming is a subset of mathematical optimization whose problems are similar to linear optimization, except that all or some problem variables are integers. Similar to linear optimization, the primary approach to integer programming is to find the minimum or maximum value of a linear function in a space with linear constraints. In the case of discrete variables, this space is not continuous and convex but a discrete space. These variables can only be 0, 1, or other valid variables.
The items considered in this modeling are demand uncertainty, reliability for an emergency response to requests, and limitation of fair time distribution and relief between stations. The studied model was solved by considering the model items (2 items according to Table 1) and indicators (9 items according to Table 2).
.jpg)
.jpg)
These items and indicators are based on the standard DSM model developed by Derrac et al. [14] (Figure 2) The study population is all data of the eastern region of Tehran (the second half of 2018). First, we tried to determine the initial points of the construction candidate in Geographic Information System (GIS) software. Then according to the criteria and their weighting by the elites, we reached the final criteria. In the final phase, the suggested sites were presented in the first stage by solving GAMS software. In general, GAMS software is one of the optimal and efficient decision-making tools in operational research. It means that wherever we need to make optimal decisions with constraints such as time, cost, and resources, we must use mathematical modeling, the components of which include 4 phases of information and data entry, model construction, analysis, and conclusion. It is used to optimize location using a genetic optimization algorithm implemented in the GAMS software environment.
In today’s real world, countless parameters may be different and uncertain. In this research, the important parameter of customer demand (dei), one of the main causes of model uncertainty, is considered an uncertain parameter. Also, fast changes in the environment have added to the uncertainty and ambiguity in the location of facilities. Therefore, to reduce the existing risk and uncertainty, it seems vital to employ an approach to deal with uncertainty. There are efficient approaches in this regard. One of these new approaches is the optimization approach, which aims to find almost insensitive solutions to the uncertainty of the environment and the changing demands. Uncertainty is used when there is no complete demand in some data, such as statistical data. To avoid measuring error, we assume an estimate and a general forecast as demand in the form of time scenarios. Reliability is used in the location of facilities in case of failure or inaccessibility of the system and to prevent disruption of system order and continued service to the applicant. In the mathematical modeling of this research, it is considered a mathematical constraint. Because of the limited capacity of ambulances to carry out missions, it is certainly not possible to complete all missions and respond to all requests. So, it is necessary to design a support base to respond to unmet requests. In general, multi-objective location means that it has three objective functions in the mathematical model. The first objective function seeks to minimize costs, the second objective function seeks to maximize coverage and demand, and the third objective function aims to minimize relief or justice time during service. In each step, one of the objective functions is solved, and the other functions are applied as constraints in the model.
Mathematical model of research
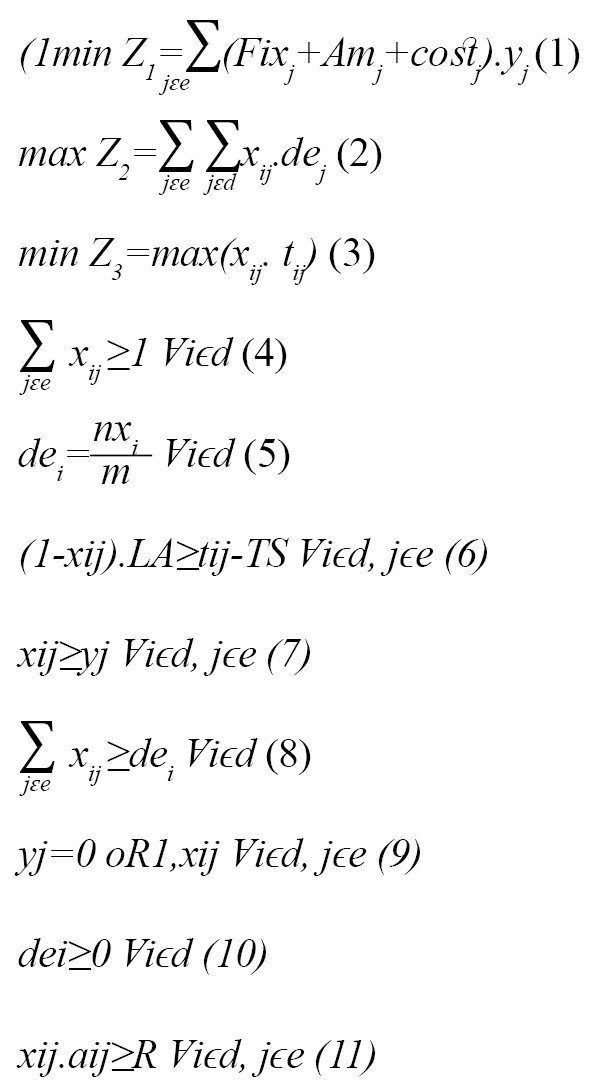
Regarding the first objective function, the fixed cost of constructing and purchasing an ambulance and the variable cost for constructed emergencies are minimized (minimizing system costs). Regarding the second objective function, the coverage radius is maximized. Regarding the third objective function, the maximum time interval for relief (to establish social justice or distribution) is minimized. The first constraint (fourth relation) ensures that at least one emergency center assists in each area (covering all locations). The second constraint (fifth relation) specifies how many emergency centers should be allocated to that area according to the demand of each area. By this constraint, the reliability of the problem is guaranteed, and based on it, the minimum number of emergency centers is determined to provide services to each area (Figure 3). The third constraint or equity in distribution (Equation 6) is that if the time interval of an emergency candidate center from an area is longer than the allowable time, then that emergency candidate center cannot be assigned to that location. In other words, the time of relief from each base to the place of demand for all ambulances sent to their place of mission must follow the same standard time. The fourth constraint (seventh relation) determines which emergency candidate center will be established. The fifth constraint (Equation 8) ensures that the minimum number of emergency rooms required for each area is assigned. The sixth constraint (ninth relation) determines the variables zero and one. The seventh constraint (tenth relation) determines the larger variables equal to zero (Equation 11). The reliability of the service ensures that all requests are made to send an ambulance and complete the mission.
The experts interviewed in this study, based on at least five years of work experience, included emergency specialists and several professors of Tehran University of Medical Sciences. The hierarchical analysis method is one of the few decision-making tools in today’s world, which is used to determine the importance of criteria and to weigh them. First, to value the criteria, each criterion was given to an expert and asked among the selected criteria in Table 3, extracted from previous studies, which of your criteria do you meet?
.jpg)
Then, these priorities were given a score from 0 to 1, and after removing the unreasonable or inconsistent scores, close numbers were selected, and the majority of opinions was applied.
3. Results
This study assumes that different areas of the city (east of Tehran) are divided into smaller regions. For each area, considering their history of demand, there is a need for relief and an emergency center. For a certain number of requests, the minimum number of emergency centers to provide services is determined. The term refers to the minimum number of ambulances available for each area, and based on this, two or more relief centers may provide services to that area. The nearest allocated emergency center is the main center, and the rest of the allocated centers are support centers (to ensure that the demand is met). Thus, it is possible to guarantee the provision of services to all demands, which will make the results of the work more realistic and bring the research closer to the real world.
Also, minimizing the maximum service time to emergency centers in different areas is considered, according to which service is balanced in all areas and justice in distribution is guaranteed. However, an area will be assigned to a relief center if the time interval between them is observed and not more than the specified time. If a relief center is needed, the cost of construction and equipment for the relief center and its running costs will be added to the system costs.
Using GIS software, the eastern part of Tehran was divided into several equal sections, of which 27 emergency relief bases are currently active. Also, 50 points were selected as primary centers, and 30 points were proposed as new emergency centers according to the factors studied in Table 3 and the genetic meta-innovative algorithm as the final proposed sites. In general, the algorithm’s main loop used first generated random responses according to the size of the population. The values of the three objective functions are then calculated for each solution. In the next step, the solutions are ranked. Finally, according to the input data, the solution to the problem is obtained according to Table 4, including the main and backup databases.
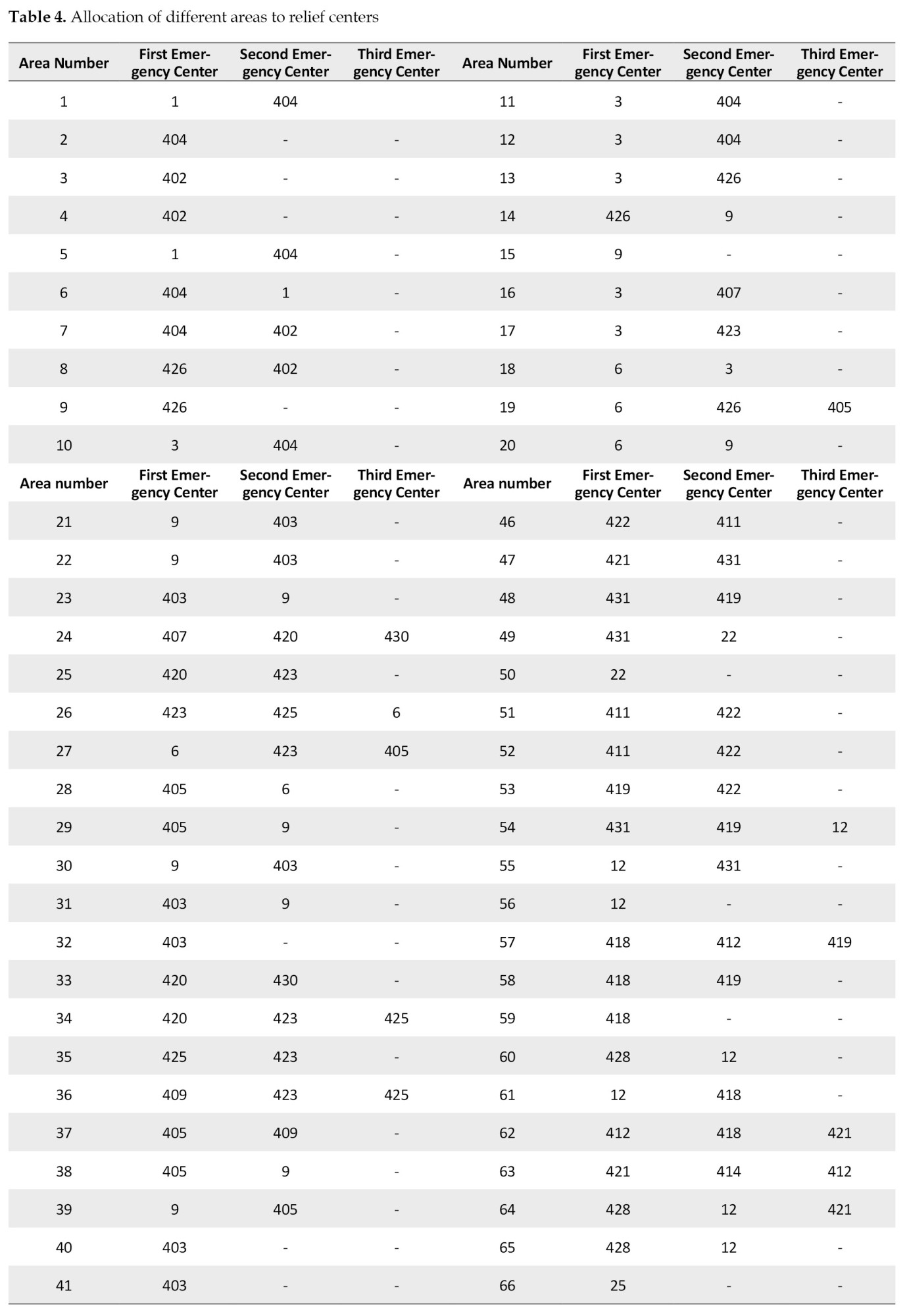
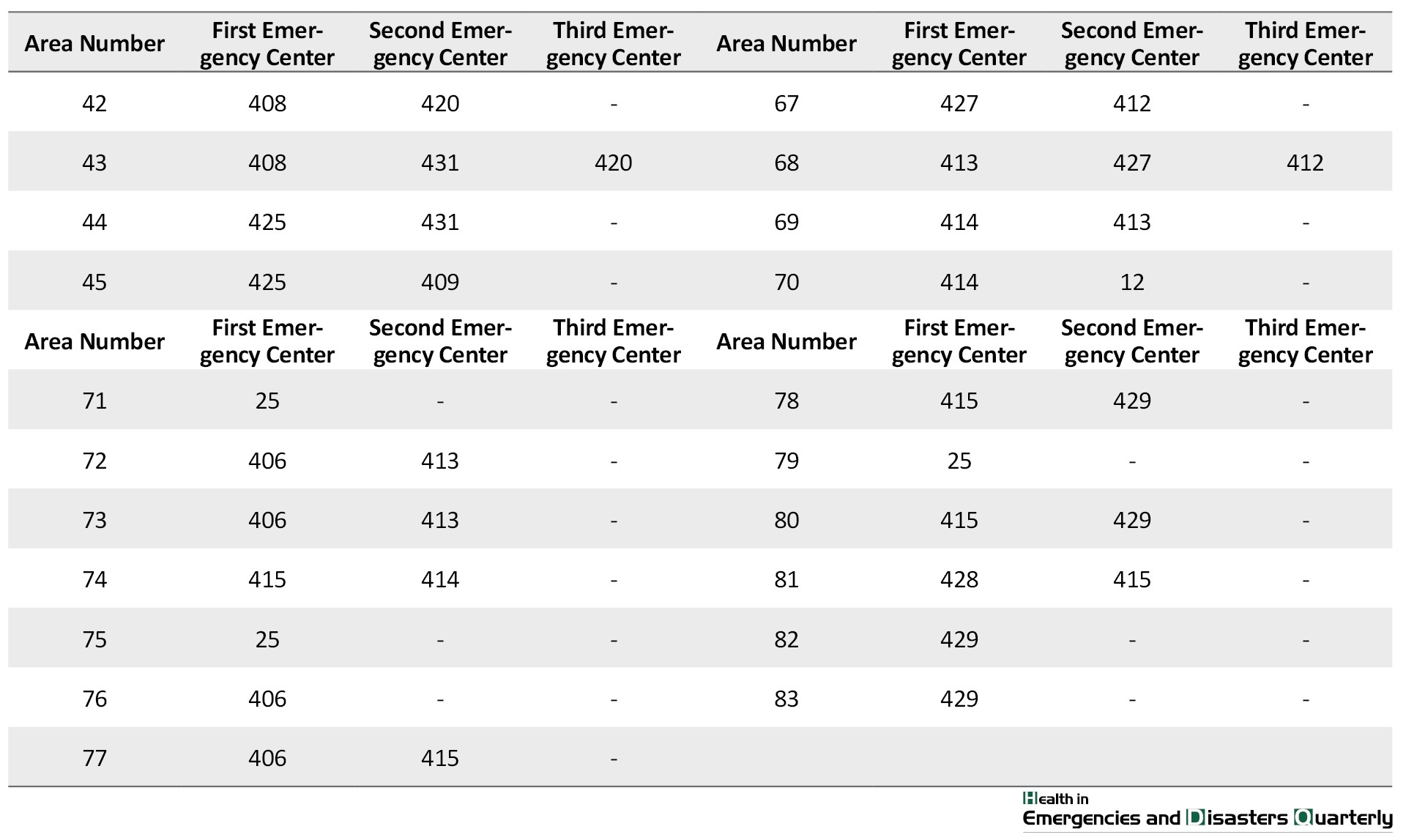
According to Table 4, the first column will be the main base of service and relief, and the second and third columns will be the support bases. If the main base (first column) cannot respond to the request, the support base will enter to carry out the mission and provide service. Using the software and the output obtained from the objective functions and constraints in the proposed mathematical model, new centers of 2, 3, 6, 9, 12, 22, and 25 are proposed for construction.
4. Discussion
This study aims to introduce and develop a mathematical model to find the optimal locations of emergency stations in Tehran in terms of variable demands and reliability. The issue of time is fundamental in an emergency. Ambulances should be on duty at all times to ensure that adequate coverage and timely response to EMS units are always available. EMS planners must choose the best locations for the dispatch of ambulances. However, it is essential to note that, despite responding to requests on time, the patient’s chances of survival are not necessarily guaranteed [11]. Excessive deviation from these standards can significantly worsen patients’ prognoses [12]. The results of this study are in line with the results of research conducted by Su and Huang in 2015, Simon 2008, Mansouri 2019, Rodrigo 2012, Sin 2010, Zarandi 2011, Davari 2011, Hali 2015, which provide a model considering the support coverage [18]. However, in the mentioned articles, location modeling is dealt with as a single purpose. The site location is modeled only with simulation software. Overlooking the different demands of the sites at any hour of the day and night is far from the reality of the real world. The lack of attention to demand uncertainty in the form of a pivotal scenario can be considered another key point of this research with previous research. Besides, considering the issues of fair distribution of ambulances, the support sites, and GIS are the innovations in this work.
5. Conclusion
Emergency stations are an essential part of any health system. The proper application of these services and their correct locations will prevent human mortality and increase the speed of relief, satisfaction, and life expectancy. Therefore, we studied the factors affecting the location of emergency centers in Tehran. In this article, indicators such as ease of access to the relief base, being in a place with high demand, being in an urban area, and being in a location near no other emergency, have been studied.
Tehran is a developing metropolis with a growing population, and in any city whose population increases, the demand for services will increase. Among these, the quality of emergency services is one of the most important services in demand. If the services and places of providing these services are chosen rationally and correctly, it can increase the desirability and satisfaction of people. This objective is possible by recognizing and examining the factors affecting the location of emergency stations. According to the research conducted in this article, the criterion of being in a place with high demand has the most weight and importance.
The number of emergency stations in East Tehran is currently 27, but using the mathematical model developed in this study, this number should be increased to 34. In other words, seven other bases are required. Using the mentioned model, the construction costs of the facility can be minimized so that the obtained solution becomes solid. This issue can have a significant effect on increasing demand coverage and thus reducing demand response time, improving quality and productivity, and especially reducing the number of deaths due to delays in relief. It should be noted that this study had some limitations, such as collecting demand data at different hours of the day.
To complete this research, we suggest that the variable of traffic effectiveness in locating bases and the subject of time in a fuzzy way be considered in future studies.
Ethical Considerations
Compliance with ethical guidelines
All authors are committed to the principle of confidentiality and identity of the interviewees and, without their consent, we are not allowed to provide this information to others.
Funding
This research did not receive any grant from funding agencies in the public, commercial, or non-profit sectors.
Authors' contributions
All authors equally contributed to preparing this article.
Conflict of interest
The authors declared no conflict of interest.
Acknowledgments
The authors appreciate the assistance of the Tehran Emergency Management Agency.
References
n today’s troubled world, where humanity faces different dangers, an accurate response system with the correct efficiency of prehospital medical emergencies is paramount. An essential feature of emergency service providers worldwide is the rapid deployment of ambulances for patients to save them. Because of the importance of saving human lives and reducing the errors caused by not sending ambulances in time and controlling the death rate, these systems should perform with high precision [1, 2].
The Emergency Medical Service (EMS) is a vital part of any health system. These services operate at a critical point in community health. In most emergencies, there is a very short golden time to provide resuscitation services, which can significantly impact disease or accident prognosis [3]. Success in the EMS system depends on the performance and skills of personnel, their knowledge, best equipment, and facilities. Because of the difficult situation of operation in EMS and the process of much information in a short time, proper decisions should be made as quickly as possible. The sooner the answer is found, the better the results for the patient [4]. Considering the high demand for these services in the east of Tehran City, Iran, and the insufficient EMS bases, the purpose of this study is to find the best places to establish emergency facilities to respond appropriately to all the requests.
Indicators of location-routing problems were determined according to “location of ambulance bases based on random demand”, “optimization of location models”, and “planning and optimization strategies” [7, 6, 5]. In this paper, all research-inspired sub-indices, a part of the sub-indices of the vehicle routing problem, were categorized into two parts: physical and structural sub-indices. In physical sub-indices, only a new constraint is added to the model affected by conditions, such as the type of transport fleet. In structural sub-indices, the set coverage model [8] or more complex possible models are considered, such as the location problem with the maximum expected coverage [9].
One of these efficient models is the Double Standard Model (DSM), used to optimize and improve the location of ambulance services in Belgium [10], Canada [11], and Austria [12]. It is one of the accepted models for related issues is locating an ambulance [13].
To provide comprehensive coverage, using reliability, proposed a distribution algorithm to reduce the number of ambulances at each base implemented and solved the DSM at different periods [14, 15, 16, 17] (Figure 1). They also modeled and solved the ambulance location problem along with the dispatch problem. In this case, the problem with the location and status of each ambulance and all emergency contacts received up to time t were defined [18]. By explaining the prioritization of location indicators, the proposed algorithm optimizes the mathematical model and determines the number and location of ambulances with the assumptions made [19].
By emphasizing the quality of services of emergency stations in New Delhi, using the statistical data of mortality during three years, and collecting data of places prone to demand, the researchers calculated and studied travel time between ambulances to the demand points [20]. In addition, the key indicators in the development of the ambulance airbase were also examined, which had the greatest impact on the distance factor [21].
Based on the research in this field and the study of location indicators in reducing mortality and growth of equitable access to health services in the reviewed articles and also the importance of health development, which is one of the indicators of country development, the primary purpose of the study is to provide an optimal plan to establish emergency stations. This plan consequently improves emergency medical services and reduces the burden of mortality, as well as shortens the response time to accidents.
2. Materials and Methods
One of the main issues for EMS is the correct location of the emergency base and the deployment of the ambulance [9]. Therefore, ambulances must be present at a particular time and distance to the requested location [10], and EMS planners should choose the best sites for establishing and deploying ambulances [11]. Researchers have found that significant deviations from these standards can worsen patients’ conditions [12]. The present study is an applied-developmental study and has used cross-sectional data of the Emergency Organization in East Tehran in 2018. A mixed-integer linear programming model was used to model the problem of optimizing emergency bases.
Integer linear programming is a subset of mathematical optimization whose problems are similar to linear optimization, except that all or some problem variables are integers. Similar to linear optimization, the primary approach to integer programming is to find the minimum or maximum value of a linear function in a space with linear constraints. In the case of discrete variables, this space is not continuous and convex but a discrete space. These variables can only be 0, 1, or other valid variables.
The items considered in this modeling are demand uncertainty, reliability for an emergency response to requests, and limitation of fair time distribution and relief between stations. The studied model was solved by considering the model items (2 items according to Table 1) and indicators (9 items according to Table 2).
.jpg)
.jpg)
These items and indicators are based on the standard DSM model developed by Derrac et al. [14] (Figure 2) The study population is all data of the eastern region of Tehran (the second half of 2018). First, we tried to determine the initial points of the construction candidate in Geographic Information System (GIS) software. Then according to the criteria and their weighting by the elites, we reached the final criteria. In the final phase, the suggested sites were presented in the first stage by solving GAMS software. In general, GAMS software is one of the optimal and efficient decision-making tools in operational research. It means that wherever we need to make optimal decisions with constraints such as time, cost, and resources, we must use mathematical modeling, the components of which include 4 phases of information and data entry, model construction, analysis, and conclusion. It is used to optimize location using a genetic optimization algorithm implemented in the GAMS software environment.
In today’s real world, countless parameters may be different and uncertain. In this research, the important parameter of customer demand (dei), one of the main causes of model uncertainty, is considered an uncertain parameter. Also, fast changes in the environment have added to the uncertainty and ambiguity in the location of facilities. Therefore, to reduce the existing risk and uncertainty, it seems vital to employ an approach to deal with uncertainty. There are efficient approaches in this regard. One of these new approaches is the optimization approach, which aims to find almost insensitive solutions to the uncertainty of the environment and the changing demands. Uncertainty is used when there is no complete demand in some data, such as statistical data. To avoid measuring error, we assume an estimate and a general forecast as demand in the form of time scenarios. Reliability is used in the location of facilities in case of failure or inaccessibility of the system and to prevent disruption of system order and continued service to the applicant. In the mathematical modeling of this research, it is considered a mathematical constraint. Because of the limited capacity of ambulances to carry out missions, it is certainly not possible to complete all missions and respond to all requests. So, it is necessary to design a support base to respond to unmet requests. In general, multi-objective location means that it has three objective functions in the mathematical model. The first objective function seeks to minimize costs, the second objective function seeks to maximize coverage and demand, and the third objective function aims to minimize relief or justice time during service. In each step, one of the objective functions is solved, and the other functions are applied as constraints in the model.
Mathematical model of research
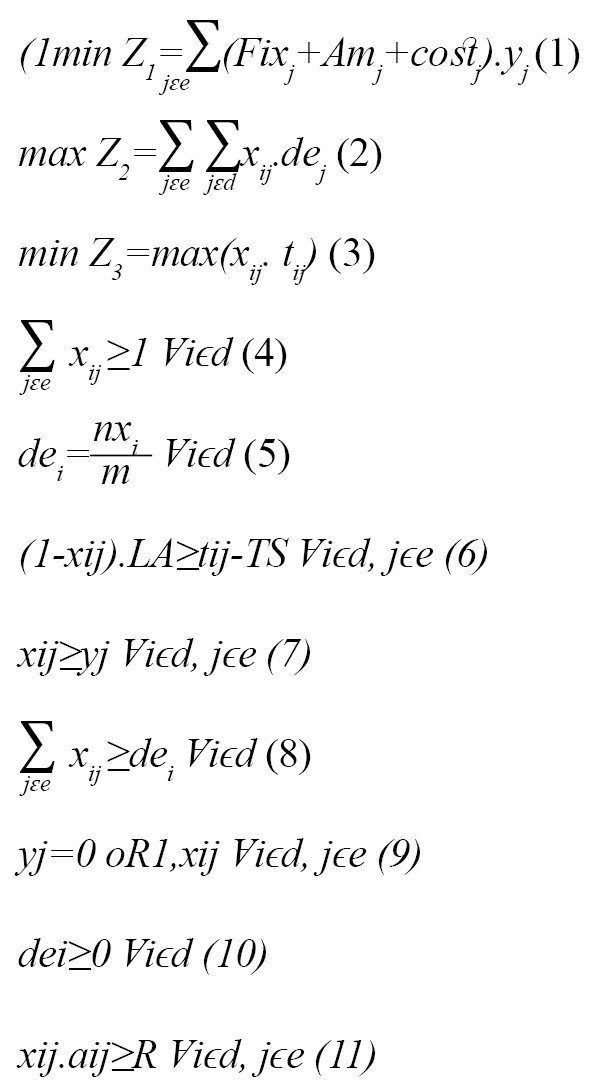
Regarding the first objective function, the fixed cost of constructing and purchasing an ambulance and the variable cost for constructed emergencies are minimized (minimizing system costs). Regarding the second objective function, the coverage radius is maximized. Regarding the third objective function, the maximum time interval for relief (to establish social justice or distribution) is minimized. The first constraint (fourth relation) ensures that at least one emergency center assists in each area (covering all locations). The second constraint (fifth relation) specifies how many emergency centers should be allocated to that area according to the demand of each area. By this constraint, the reliability of the problem is guaranteed, and based on it, the minimum number of emergency centers is determined to provide services to each area (Figure 3). The third constraint or equity in distribution (Equation 6) is that if the time interval of an emergency candidate center from an area is longer than the allowable time, then that emergency candidate center cannot be assigned to that location. In other words, the time of relief from each base to the place of demand for all ambulances sent to their place of mission must follow the same standard time. The fourth constraint (seventh relation) determines which emergency candidate center will be established. The fifth constraint (Equation 8) ensures that the minimum number of emergency rooms required for each area is assigned. The sixth constraint (ninth relation) determines the variables zero and one. The seventh constraint (tenth relation) determines the larger variables equal to zero (Equation 11). The reliability of the service ensures that all requests are made to send an ambulance and complete the mission.
The experts interviewed in this study, based on at least five years of work experience, included emergency specialists and several professors of Tehran University of Medical Sciences. The hierarchical analysis method is one of the few decision-making tools in today’s world, which is used to determine the importance of criteria and to weigh them. First, to value the criteria, each criterion was given to an expert and asked among the selected criteria in Table 3, extracted from previous studies, which of your criteria do you meet?
.jpg)
Then, these priorities were given a score from 0 to 1, and after removing the unreasonable or inconsistent scores, close numbers were selected, and the majority of opinions was applied.
3. Results
This study assumes that different areas of the city (east of Tehran) are divided into smaller regions. For each area, considering their history of demand, there is a need for relief and an emergency center. For a certain number of requests, the minimum number of emergency centers to provide services is determined. The term refers to the minimum number of ambulances available for each area, and based on this, two or more relief centers may provide services to that area. The nearest allocated emergency center is the main center, and the rest of the allocated centers are support centers (to ensure that the demand is met). Thus, it is possible to guarantee the provision of services to all demands, which will make the results of the work more realistic and bring the research closer to the real world.
Also, minimizing the maximum service time to emergency centers in different areas is considered, according to which service is balanced in all areas and justice in distribution is guaranteed. However, an area will be assigned to a relief center if the time interval between them is observed and not more than the specified time. If a relief center is needed, the cost of construction and equipment for the relief center and its running costs will be added to the system costs.
Using GIS software, the eastern part of Tehran was divided into several equal sections, of which 27 emergency relief bases are currently active. Also, 50 points were selected as primary centers, and 30 points were proposed as new emergency centers according to the factors studied in Table 3 and the genetic meta-innovative algorithm as the final proposed sites. In general, the algorithm’s main loop used first generated random responses according to the size of the population. The values of the three objective functions are then calculated for each solution. In the next step, the solutions are ranked. Finally, according to the input data, the solution to the problem is obtained according to Table 4, including the main and backup databases.


According to Table 4, the first column will be the main base of service and relief, and the second and third columns will be the support bases. If the main base (first column) cannot respond to the request, the support base will enter to carry out the mission and provide service. Using the software and the output obtained from the objective functions and constraints in the proposed mathematical model, new centers of 2, 3, 6, 9, 12, 22, and 25 are proposed for construction.
4. Discussion
This study aims to introduce and develop a mathematical model to find the optimal locations of emergency stations in Tehran in terms of variable demands and reliability. The issue of time is fundamental in an emergency. Ambulances should be on duty at all times to ensure that adequate coverage and timely response to EMS units are always available. EMS planners must choose the best locations for the dispatch of ambulances. However, it is essential to note that, despite responding to requests on time, the patient’s chances of survival are not necessarily guaranteed [11]. Excessive deviation from these standards can significantly worsen patients’ prognoses [12]. The results of this study are in line with the results of research conducted by Su and Huang in 2015, Simon 2008, Mansouri 2019, Rodrigo 2012, Sin 2010, Zarandi 2011, Davari 2011, Hali 2015, which provide a model considering the support coverage [18]. However, in the mentioned articles, location modeling is dealt with as a single purpose. The site location is modeled only with simulation software. Overlooking the different demands of the sites at any hour of the day and night is far from the reality of the real world. The lack of attention to demand uncertainty in the form of a pivotal scenario can be considered another key point of this research with previous research. Besides, considering the issues of fair distribution of ambulances, the support sites, and GIS are the innovations in this work.
5. Conclusion
Emergency stations are an essential part of any health system. The proper application of these services and their correct locations will prevent human mortality and increase the speed of relief, satisfaction, and life expectancy. Therefore, we studied the factors affecting the location of emergency centers in Tehran. In this article, indicators such as ease of access to the relief base, being in a place with high demand, being in an urban area, and being in a location near no other emergency, have been studied.
Tehran is a developing metropolis with a growing population, and in any city whose population increases, the demand for services will increase. Among these, the quality of emergency services is one of the most important services in demand. If the services and places of providing these services are chosen rationally and correctly, it can increase the desirability and satisfaction of people. This objective is possible by recognizing and examining the factors affecting the location of emergency stations. According to the research conducted in this article, the criterion of being in a place with high demand has the most weight and importance.
The number of emergency stations in East Tehran is currently 27, but using the mathematical model developed in this study, this number should be increased to 34. In other words, seven other bases are required. Using the mentioned model, the construction costs of the facility can be minimized so that the obtained solution becomes solid. This issue can have a significant effect on increasing demand coverage and thus reducing demand response time, improving quality and productivity, and especially reducing the number of deaths due to delays in relief. It should be noted that this study had some limitations, such as collecting demand data at different hours of the day.
To complete this research, we suggest that the variable of traffic effectiveness in locating bases and the subject of time in a fuzzy way be considered in future studies.
Ethical Considerations
Compliance with ethical guidelines
All authors are committed to the principle of confidentiality and identity of the interviewees and, without their consent, we are not allowed to provide this information to others.
Funding
This research did not receive any grant from funding agencies in the public, commercial, or non-profit sectors.
Authors' contributions
All authors equally contributed to preparing this article.
Conflict of interest
The authors declared no conflict of interest.
Acknowledgments
The authors appreciate the assistance of the Tehran Emergency Management Agency.
References
- Dami F, Golay C, Pasquier M, Fuchs V, Carron PN, Hugli O. Prehospital triage accuracy in a criteria based dispatch centre. BMC Emergency Medicine. 2019; 15:32. [DOI:10.1186/s12873-015-0058-x] [PMID] [PMCID]
- Bohm K, Kurland L. The accuracy of medical dispatch - a systematic review. Scandinavian Journal of Trauma Resuscitation and Emergency Medicine. 2018; 26(1):94. [DOI:10.1186/s13049-018-0528-8] [PMID] [PMCID]
- Vafaee nasab M, Fateh panah A, Jahangiri K, Namdari M. [Evaluation of Yazd pre-hospital emergency pegasys performance based on duration of patient presentation (Persian)]. Toloe Behdasht. 2017; 15(5):122-31. http://tbj.ssu.ac.ir/article-1-1103-fa.html
- Zarratchi A, Rostami B, Rostami A. [Temporal characteristics of pre-hospital emergency services; A cross-sectional study (Persian)]. Iranian Journal of Emergency Medicine. 2016; 5(1):e8. [DOI:10.22037/ijem.v2i1.18192]
- Laporte G, Nickel S, Saldanha da Gama F. Location Science. 1st ed. Berlin: Springer; 2015. [DOI:10.1007/978-3-319-13111-5]
- Simon D. Biogeography-based optimization. IEEE Transactions on Evolutionary Computation. 2008; 12(6):702-13. [DOI:10.1109/TEVC.2008.919004]
- Mansouri N, Mohammad Hasani Zade B, Javidi MM. Hybrid task scheduling strategy for cloud computing by modified particle swarm optimization and fuzzy theory. Computers & Industrial Engineering. 2019; 130:597-633. [DOI:10.1016/j.cie.2019.03.006]
- Atta S, Mahapatra PRS, Mukhopadhyay A. Solving maximal covering location problem using genetic algorithm with local refinement. Soft Computing. 2018; 22(12):3891-906. [DOI:10.1007/s00500-017-2598-3]
- Cordeau JF, Furini F, Ljubić I. Benders decomposition for very large scale partial set covering and maximal covering location problems. European Journal of Operational Research. 2019; 275(3):882-96. [DOI:10.1016/j.ejor.2018.12.021]
- Zhen L, Wang K, Hu H, Chang D. A simulation optimization framework for ambulance deployment and relocation problems. Computers & Industrial Engineering. 2014; 72:12-23. [DOI:10.1016/j.cie.2014.03.008]
- Su Q, Luo Q, Huang SH. Cost-effective analyses for emergency medical services deployment: A case study in Shanghai. International Journal of Production Economics. 2015; 163:112-23. [DOI:10.1016/j.ijpe.2015.02.015]
- Van den Berg PL, Kommer GJ, Zuzáková B. Linear formulation for the maximum expected coverage location model with fractional coverage. Operations Research for Health Care. 2016; 8:33-41. [DOI:10.1016/j.orhc.2015.08.001]
- Shariff SR, Moin NH, Omar M. Location allocation modeling for healthcare facility planning in Malaysia. Computers & Industrial Engineering. 2012; 62(4):1000-10. [DOI:10.1016/j.cie.2011.12.026]
- Derrac J, García S, Molina D, Herrera F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm and Evolutionary Computation. 2011; 1(1):3-18. [DOI:10.1016/j.swevo.2011.02.002]
- Rodriguez FJ, Blum C, Lozano M, García-Martínez C. Iterated greedy algorithms for the maximal covering location problem. European Conference on Evolutionary Computation in Combinatorial Optimization, 2012, Berlin, Germany. [DOI:10.1007/978-3-642-29124-1_15]
- Senne ELF, Pereira MA, Lorena LAN. A decomposition heuristic for the maximal covering location problem. Advances in Operations Research. 2010; 2010:120756. [DOI:10.1155/2010/120756]
- Zarandi MF, Davari S, Sisakht SH. The large scale maximal covering location problem. Scientia Iranica. 2011; 18(6):1564-70. [DOI:10.1016/j.scient.2011.11.008]
- Davari S, Zarandi MHF, Hemmati A. Maximal covering location problem (MCLP) with fuzzy travel times. Expert Systems with Applications. 2011; 38(12):14535-41. [DOI:10.1016/j.eswa.2011.05.031]
- Helle KB, Pebesma E. Optimising sampling designs for the maximum coverage problem of plume detection. Spatial Statistics. 2015; 13:21-44. [DOI:10.1016/j.spasta.2015.03.004]
- Wajid S, Nezamuddin N, Unnikrishnan A. Optimizing ambulance locations for coverage enhancement of accident sites in South Delhi. Transportation Research Procedia. 2020; 48():280-9. https://pdf.sciencedirectassets.com/308315/1-s2.0-S2352146520X0007X/1-s2.0-S235214652
- Eskandari, Zahra, Nouri F, Khorasani-Zavareh D, Ghomian Z. [Factors contributing to the development of air ambulance base: A protocol for systematic review (Persian)]. Journal of Complementary Medicine Research. 2021; 12.(1):1-4. https://www.ejmanager.com/mnstemps/55/55-1603184158.pdf?t=1635160380
Type of article: Applicable |
Subject:
Special
Received: 2021/04/24 | Accepted: 2021/07/17 | Published: 2021/07/1
Received: 2021/04/24 | Accepted: 2021/07/17 | Published: 2021/07/1
Send email to the article author
| Rights and permissions | |
 |
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License. |








.jpg)
.jpg)
.jpg)
