Volume 10, Issue 3 (Spring 2025)
Health in Emergencies and Disasters Quarterly 2025, 10(3): 193-206 |
Back to browse issues page
Download citation:
BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:



BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:
Eskandari T, Mohammadfam I. Application of Fuzzy Bayesian Network in Dynamic Risk Analysis of Explosion in Process Industries. Health in Emergencies and Disasters Quarterly 2025; 10 (3) :193-206
URL: http://hdq.uswr.ac.ir/article-1-622-en.html
URL: http://hdq.uswr.ac.ir/article-1-622-en.html
1- Department of Occupational Health, Occupational Health and Safety Research Center, School of Public Health, Hamadan University of Medical Sciences, Hamadan, Iran. & Department of Occupational Health Engineering, School of Public Health, Iran University of Medical Sciences, Tehran, Iran.
2- Department of Ergonomics, Health in Emergency and Disaster Research Center, School of Rehabilitation Sciences, University of Social Welfare and Rehabilitation Sciences, Tehran, Iran. ,ir.mohammadfam@uswr.ac.ir
2- Department of Ergonomics, Health in Emergency and Disaster Research Center, School of Rehabilitation Sciences, University of Social Welfare and Rehabilitation Sciences, Tehran, Iran. ,
Full-Text [PDF 1989 kb]
(737 Downloads)
| Abstract (HTML) (2335 Views)
Full-Text: (516 Views)
Introduction
Process industries, characterized by high equipment density, hazardous materials, a large workforce, process complexity, and significant potential for accidents and catastrophic consequences, are classified as complex systems [1]. In the process industries, human factors have been identified as one of the most common causes of catastrophic accidents [2]. The reason for this conclusion can be the large number of employees in these industries [1, 2]. Additionally, the substantial quantities of flammable hydrocarbons typically stored in these industries amplify the risk of catastrophic events with far-reaching consequences: Financial, life-threatening, and environmental [2, 3]. In the meantime, fires and explosions can cause significant damage [4, 5]. In the recent fire and explosion catastrophic accidents in Texas Refinery in March 2005, 15 people were killed, 180 people were injured, and a financial loss of 1.5 billion USD was left [6]. In the horrible explosion in Toronto Propane storage facilities in 2008, 2 people were killed, and thousands of people were evacuated. Moreover, in the horrible fire and explosion in the British Petroleum Deepwater Horizon sea platform due to oil leakage in 2010, 11 people were killed, and financial and environmental losses of 36.9 billion USD were made [6].
These accidents prompted safety experts to prioritize upgrading safety systems and conducting risk-based studies to implement appropriate control measures. Given the significant losses resulting from numerous fire and explosion accidents in process industries, establishing a decision-making standard and prioritizing hazards has become necessary. Consequently, decision-making and management now rely on risk assessment [2, 7].
Risk analysis serves as a crucial tool for formulating accident prevention strategies and practical risk mitigation measures within complex systems. Simultaneously, its primary objective is to yield actionable insights to inform accident prevention efforts or mitigate the severity of accident consequences [8].
Various methods are employed to identify and evaluate risks. The choice of an appropriate approach hinges on factors such as available data, industry context, desired outcomes, financial limitations, and time constraints [9]. In process industries, traditional risk assessment methods include fault tree analysis (FTA), event tree analysis (ETA), and bowtie technique [10-12]. These approaches depend on imperfect, non-specific data, which can introduce uncertainty into the results due to their lack of relevance to the specific plant under study and its outdated nature [13]. Consequently, discovering a technique to minimize the uncertainty associated with the prior failure rate of fundamental events holds great importance. Fuzzy logic is suggested to reduce uncertainty in estimating the probability of basic event occurrences. Numerous studies have demonstrated that the fuzzy approach can be instrumental when dealing with events lacking sufficient data for calculating occurrence probabilities in their databases [14, 15]. Traditional risk assessment methods often grapple with the challenge of staticity. Consequently, they struggle to effectively analyze the risks associated with dynamic systems [16-18]. In process industries, the Bayesian network (BN) serves as an excellent tool for conducting quantitative analyses [17]. A BN provides a probabilistic approach to handling uncertainty and can mitigate the limitations of traditional methods. It considers conditional dependencies, common defects, and various modes of basic events during the risk assessment process. One of the key benefits of BNs lies in their capacity to update probabilities, making it an excellent approach for assessing risk in dynamic systems [19, 20].
The primary objective of this study is to conduct an explosion risk analysis of a tank employed in an industrial process. This study uses a combination of tools: The bowtie diagram is used for analyzing the causes and consequences of a specific scenario, an approach using fuzzy logic to assess the likelihood of essential events, and BNs are used to discern the nature and patterns of connections among the contributing factors behind catastrophic events.
Materials and Methods
The current cross-sectional study investigated the process industry. The gas storage tank under study was chosen due to its historical records of past events and crucial role in maintaining normal process operations. This study conducted a probabilistic risk assessment of gas storage tank, gas leakage, fire, and explosion using the Bayesian tree (BT) model and Fuzzy-BN (FBN). The study steps were as follows.
Bowtie technique
The bowtie analysis is a graphical method that illustrates the complete sequence of events leading to an accident. It begins by identifying the causes of the accident and traces them through to their potential consequences. BT combines FTA and ETA to provide a comprehensive view of the risk [21, 22].
Investigating the primary factors behind the chosen scenario (the top event) involved applying the FTA method. This structured and hierarchical method illustrates how an undesirable accident can arise by linking intermediate and basic events. In FTA, the undesired accident is typically identified as the top event. This approach illustrates the relationships between events and their causes through logical ‘AND’ and ‘OR’ gateways [23, 24]. The ETA approach was employed to assess potential consequences that might arise in the event of a top-event incident and the failure of each safety barrier. At each stage of the event tree, the final implications due to the occurrence of the top event are determined by creating two branches of success and failure related to safety [25]. This study employed a combination of direct observation, expert interviews, and document and operational map review.
Fuzzy approach
In most risk analysis studies, the probability of basic events occurring is extracted from the defect rate of the events databases. This information may not be up-to-date on the desired event. Also, the defect rate of the desired event is often not accurately found, and similar event data should be used. This condition causes considerable uncertainty in data and results [26, 27]. In this research, fuzzy logic is applied to mitigate the uncertainty associated with the probability of essential events occurring in the developed FTA model. There are five steps for calculating the probability of failure for each crucial event. These steps begin with selecting a team of experts and end with the probability estimate. Probability estimation is often achieved by applying the trapezoidal and Onisawa formulas.
Step 1: Expert selection
The expert’s opinion is used when there is not enough information. In this study, an expert is someone who has complete information about the system and is familiar with FTA and ETA methods. Five experts were appointed in this study.
Step 2: Weighing the experts
Knowing that the experts have different criteria such as job title, education, years of related experience, etc. a relative weighting factor was determined based on the Likert score scale to apply the probability of basic events occurrence (Table 1).
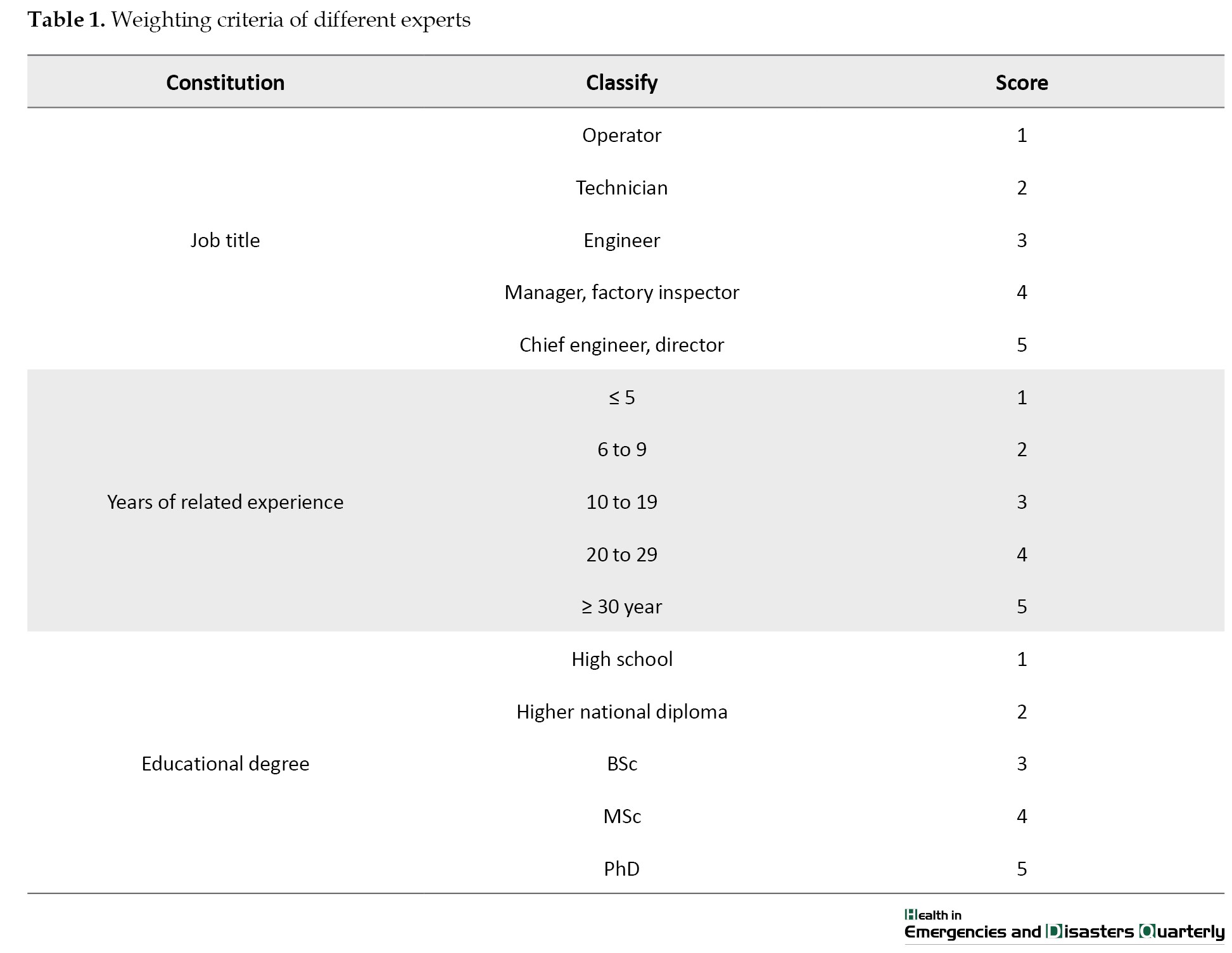
Referring to Table 1, the relative weighting factor for each expert consists of the sum of the Likert scores gained by each expert divided by the sum of the scores gained by all experts [28, 29].
Step 3: Quantification
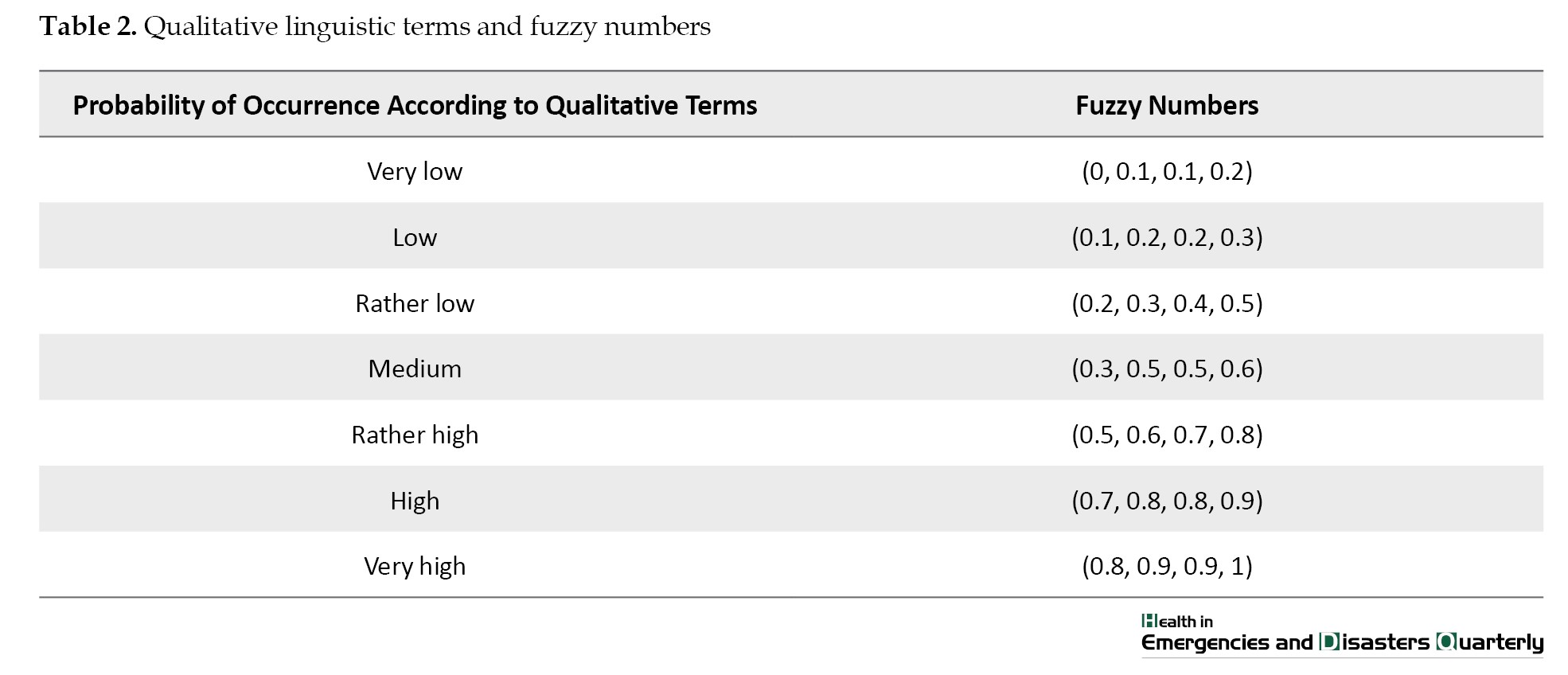
Seven language terms and trapezoidal functions (Table 2) were used to quantify experts’ opinions on essential events.
Chen and Hwang’s method was employed to quantify experts’ opinions [30].
Then, experts’ opinions were integrated based on the study conducted by Clemen and Winkler [31] and using fuzzy number theory and Equation 1:
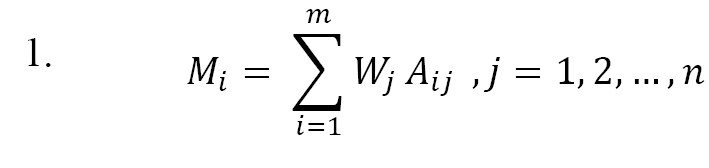
, where Wj is the weight of expert j, Aij is the linguistic term set by the expert j to the event i, j is the number of experts, and Mi is the integrated experts’ opinion (fuzzy probability of basic event i failure).
Step 4: De-fuzzing
In this stage, the obtained numbers, which are equivalent to the experts’ opinion and still in “probable” mode, became de-fuzzy using the Equation of gravitation center (trapezoid) (Equation 2) [32].
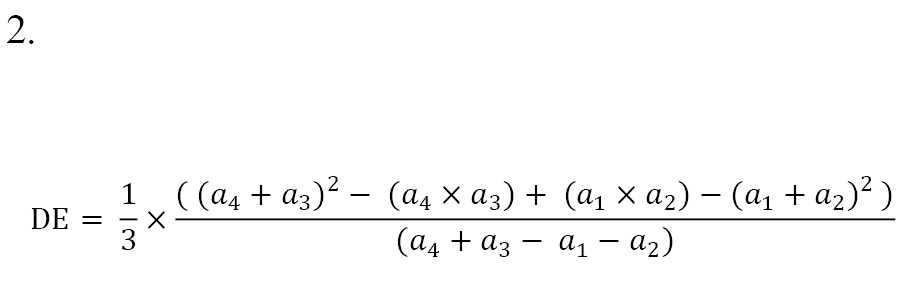
Step 5: Converting probable numbers to probabilities
The numbers obtained from the de-fuzzing step are still in the “probable” mode. Since the fault tree accepts probability, the obtained numbers must be converted from probable to probability. For this purpose, Onisawa formula and Equations 3 and 4 are used [33, 34].
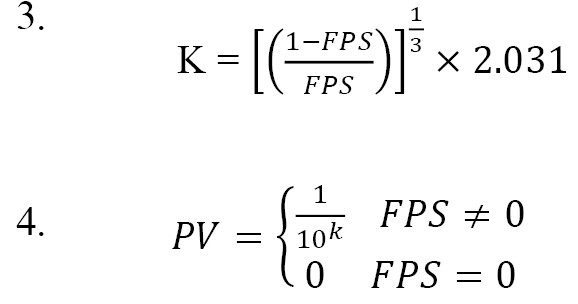
Although fuzzy theory can significantly reduce uncertainty, it cannot perform deductive reasoning (probability update) in the structure of the used fuzzy methods, such as fuzzy FTA and fuzzy BT model [35]. This study used the BN’s logic to overcome this limitation.
BN
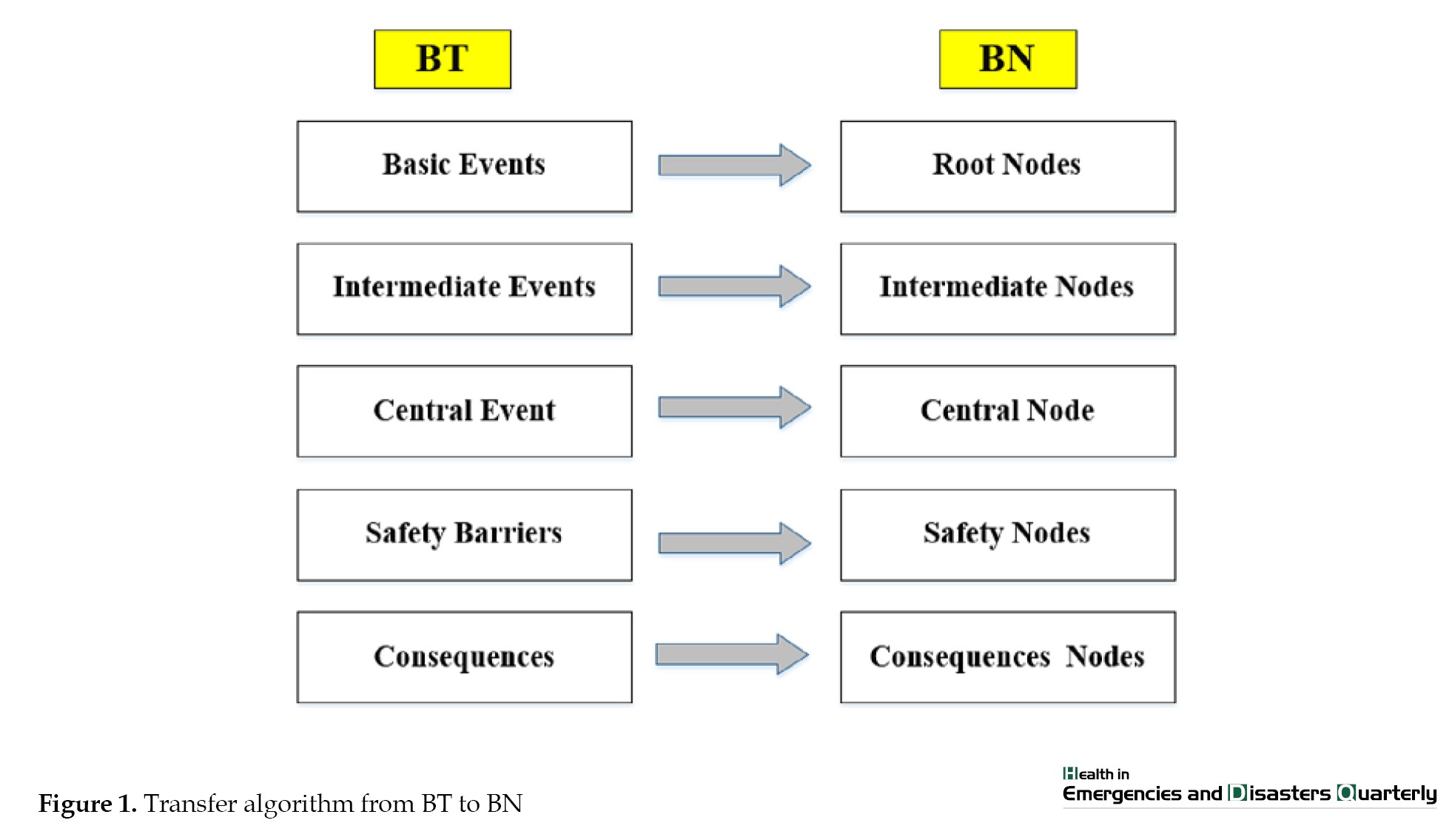
After constructing the scenario using the BT model and assessing the probabilities of essential events and safety barriers through fuzzy logic, the resulting model was migrated to the BN framework to address its shortcomings and limitations. The transfer algorithm (mapping) from the BT model to the BN was developed based on research conducted by Khakzad et al [17]. A Bayesian BT model was developed and analyzed using GeNIe software for this study. Figure 1 illustrates the algorithm for transferring data BT to the BN. The basic events, intermediate events, central events, safety barriers, and consequences in the BT model are respectively mapped to root nodes, intermediate nodes, central nodes, safety barrier nodes, and consequence nodes in the BN model.
To quantify the model, fuzzy probabilities of essential events were used as root node probabilities. In BN models, conditional probability distribution tables are employed to estimate the probability of intermediate events. The probability of an intermediate node is calculated based on the conditional dependencies between the root nodes and the probabilistic conditional relations for all possible states of the node variables. The probability of the central node was determined using the same method. Equation 5 was applied to the BN to calculate the joint probability distribution of the set of variables U = (x1, ..., xn).
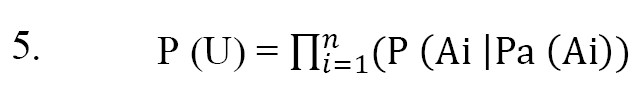
, where Pa (Ai) is the parent set of Ai in BN, and P (U) represents the properties of the BN [17, 36].
The most effective basic events were identified after creating a qualitative and quantitative model for the selected scenario using probability update features (nodes and consequences) and conducting a sensitivity analysis. In diagnostic analysis, BNs employ Bayes’ theorem to update prior probabilities based on new observations from a distinct set of variables known as evidence (often denoted as ‘E’). The probability distribution can be computed using various inference algorithms, including connection tree and variable elimination, grounded in Bayes’ theorem (Equation 6).
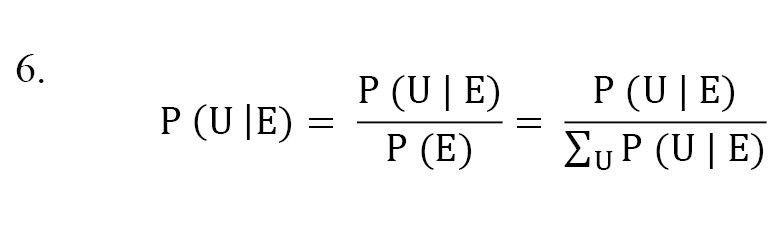
Sensitivity analysis
Sensitivity analysis was done using the rate of variation (RoV) approach.
RoV approach
The rate of variation is used to select the most effective essential events and minimal cut sets (MCSs) [37]. The RoV value is determined by Equations 7 and 8.
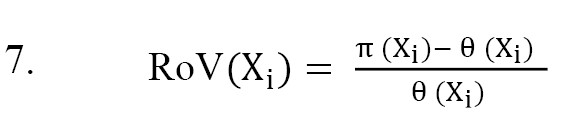
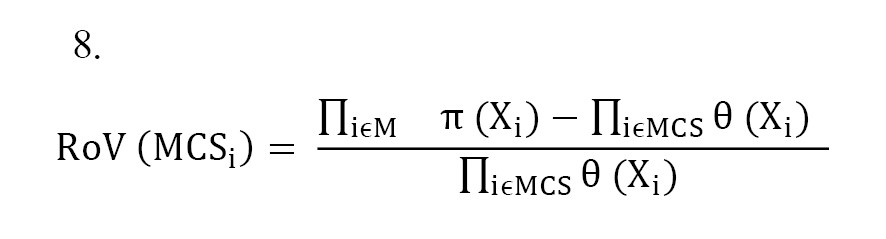
, where, π (Xi) and θ (Xi) represent the posterior and prior probabilities of the Xi essential event, respectively, and and represent posterior and prior probabilities, respectively.
Results
Drawing the BT diagram
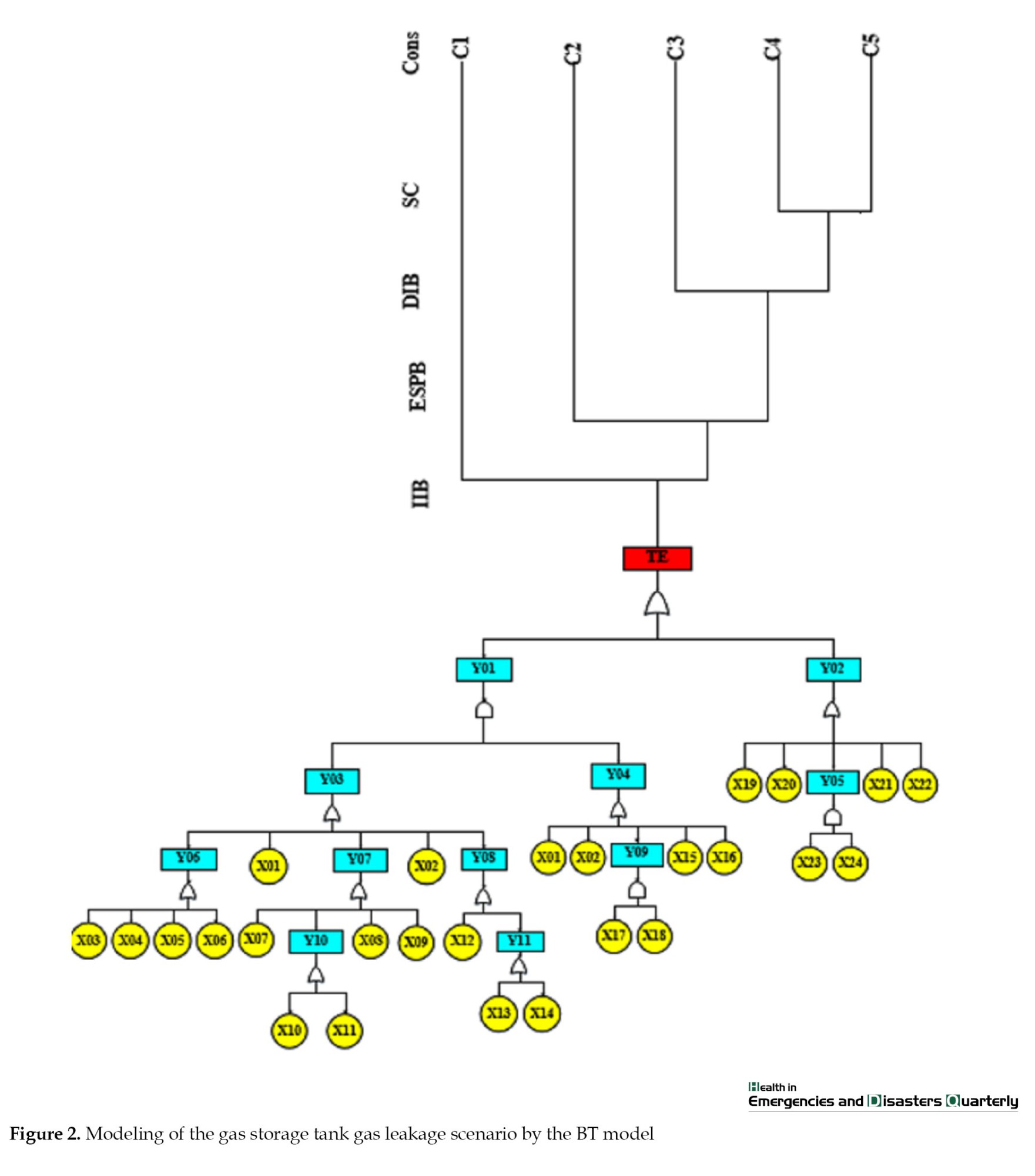
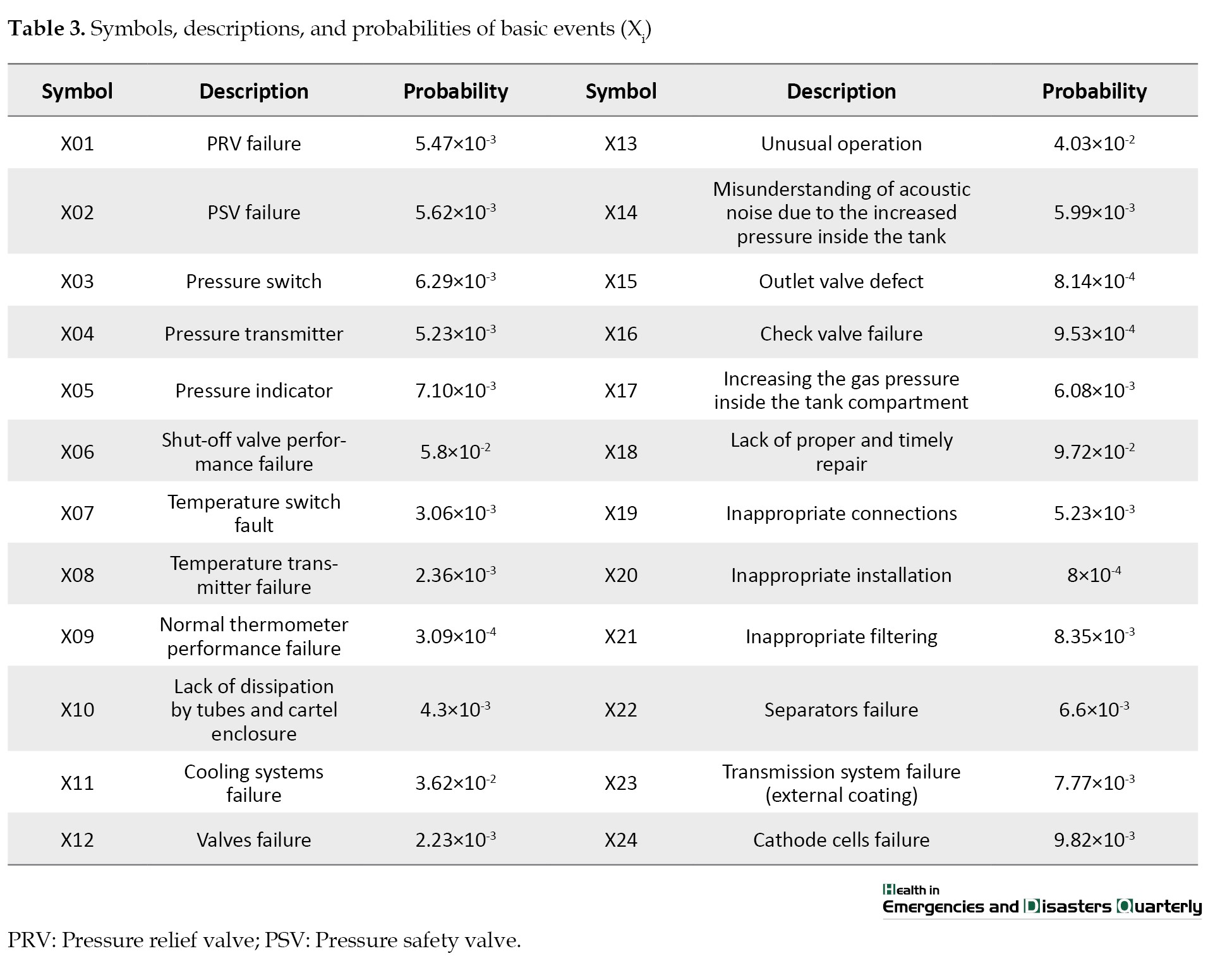
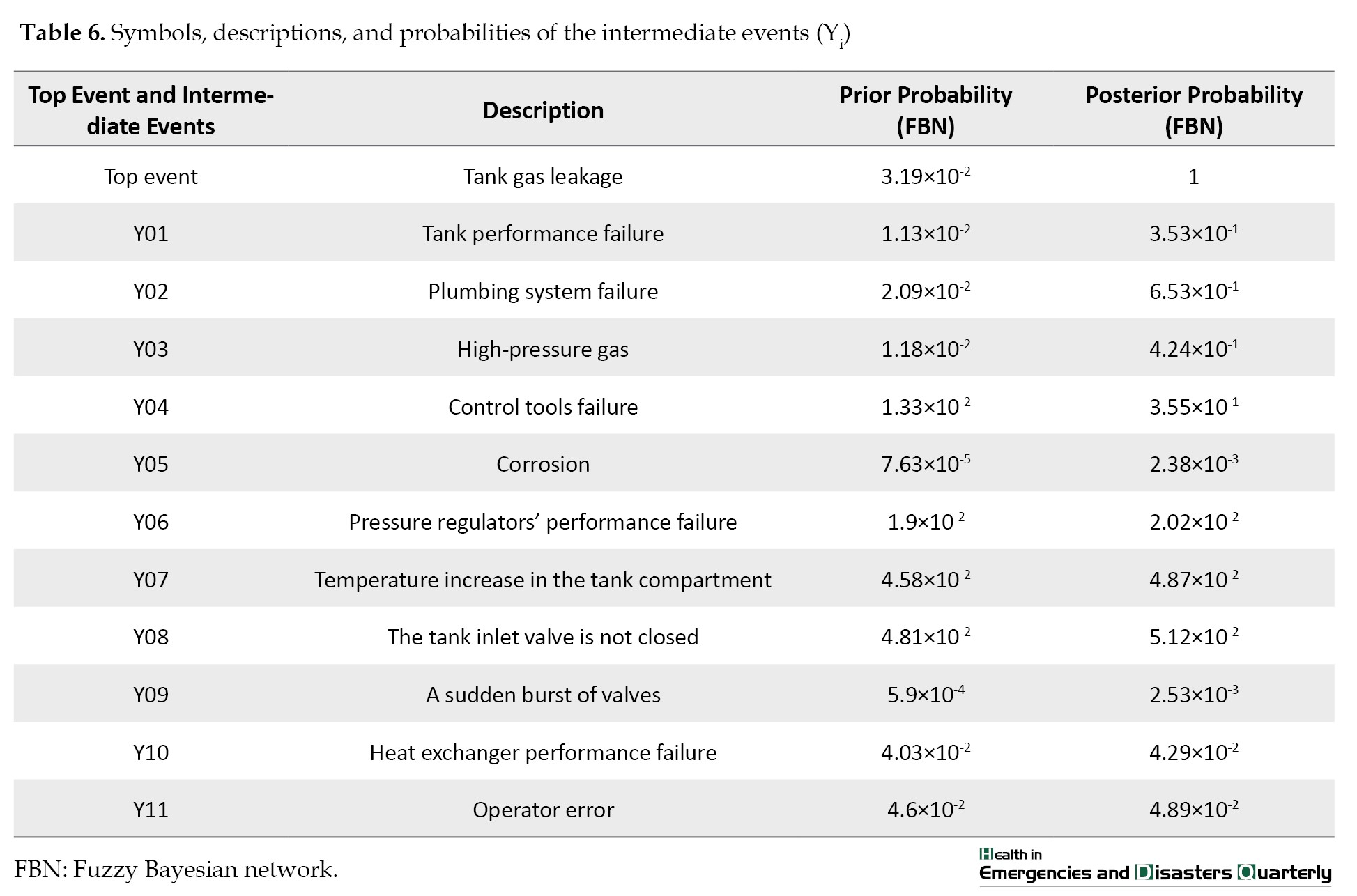
The BT diagram of the gas storage tank gas leakage scenario is presented in Figure 2, where the FTA is located on the left side, and the ETA is on the right. The fault tree associated with the gas storage tank gas leak (top event) indicates that tank performance and plumbing system failure were identified as the main intermediate causes. These causes were categorized as intermediate and basic events. The symbols, descriptions, and probabilities of the basic events are presented in Table 3.
The event tree section was drawn considering four safety barriers: Immediate ignition barrier, emergency stop pushes button, delay ignition barrier, and space confinement, to sequence the events after the top event occurrence. The first and second columns of Table 4 show the symbols, descriptions, and defect probabilities of safety barriers.

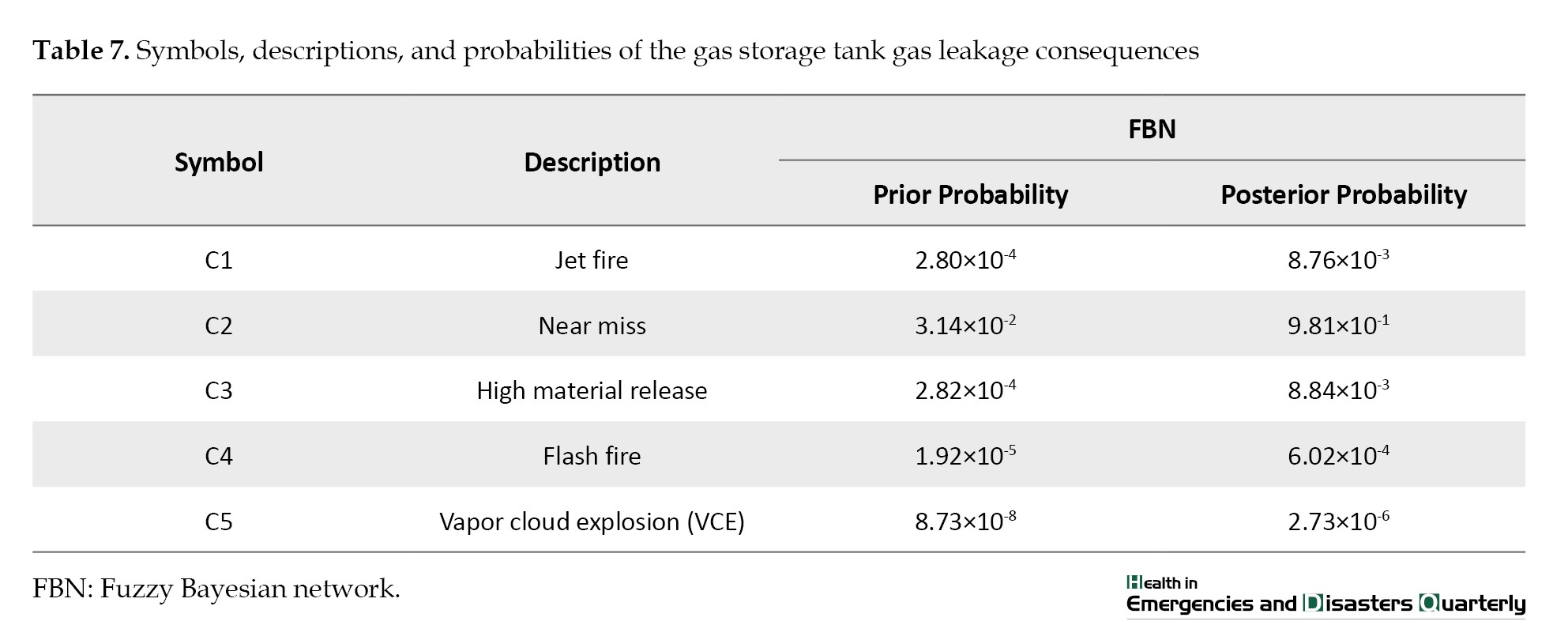
Considering the performance of the safety barriers, either failure or proper and expected operation, the gas storage tank leakage scenario led to five ultimate consequences, including flash fire, jet fire, vapor cloud explosion, release of materials, and near miss.
The probability of delayed ignition rises with the expansion of the gas vapor cloud and, consequently, the volume of the released gas. Given that the emergency stop push button (ESPB) failure typically results in a larger gas release, the probability of delayed ignition is correspondingly higher (Table 4).
Calculating fuzzy probabilities for basic events and safety barriers
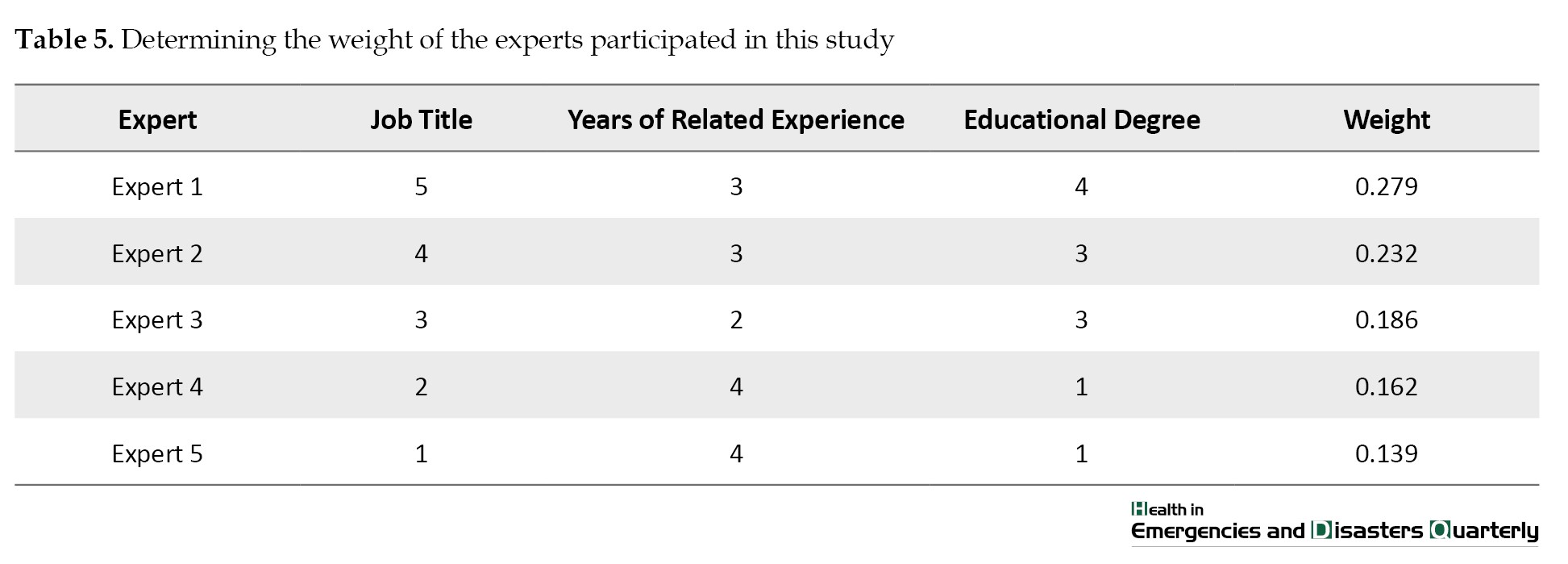
At the outset, a panel of five qualified experts, a chief engineer, a manager, a process engineer, an operational technician, and an operator, was chosen to assess the probability of basic event occurrences. Based on the established criteria for scoring the weight of experts, as outlined in Table 1, the weight of each expert involved in the study was determined, and the results are presented in Table 5.
The linguistic terms in Table 2 were used to gather expert opinions on the probability of essential events and safety barriers failing to prevent the scenario. Moreover, the experts’ views were integrated using Equation 1, and then the experts’ opinions were subjected to a de-fuzzy operation. The fuzzy probability score calculated the number obtained by de-fuzzing each basic event. Finally, the probabilistic numbers (de-fuzzing) were converted into probability values by Equations 3 and 4. The calculation was applied to all 24 basic events, resulting in the identification of the tank gas leak scenario and the safety barriers relevant to preventing its occurrence. Finally, the fuzzy logic approach was used to determine the probability of failure for each basic event. The fuzzy logic outcomes are presented in the third column of Tables 6 and 7.
BN
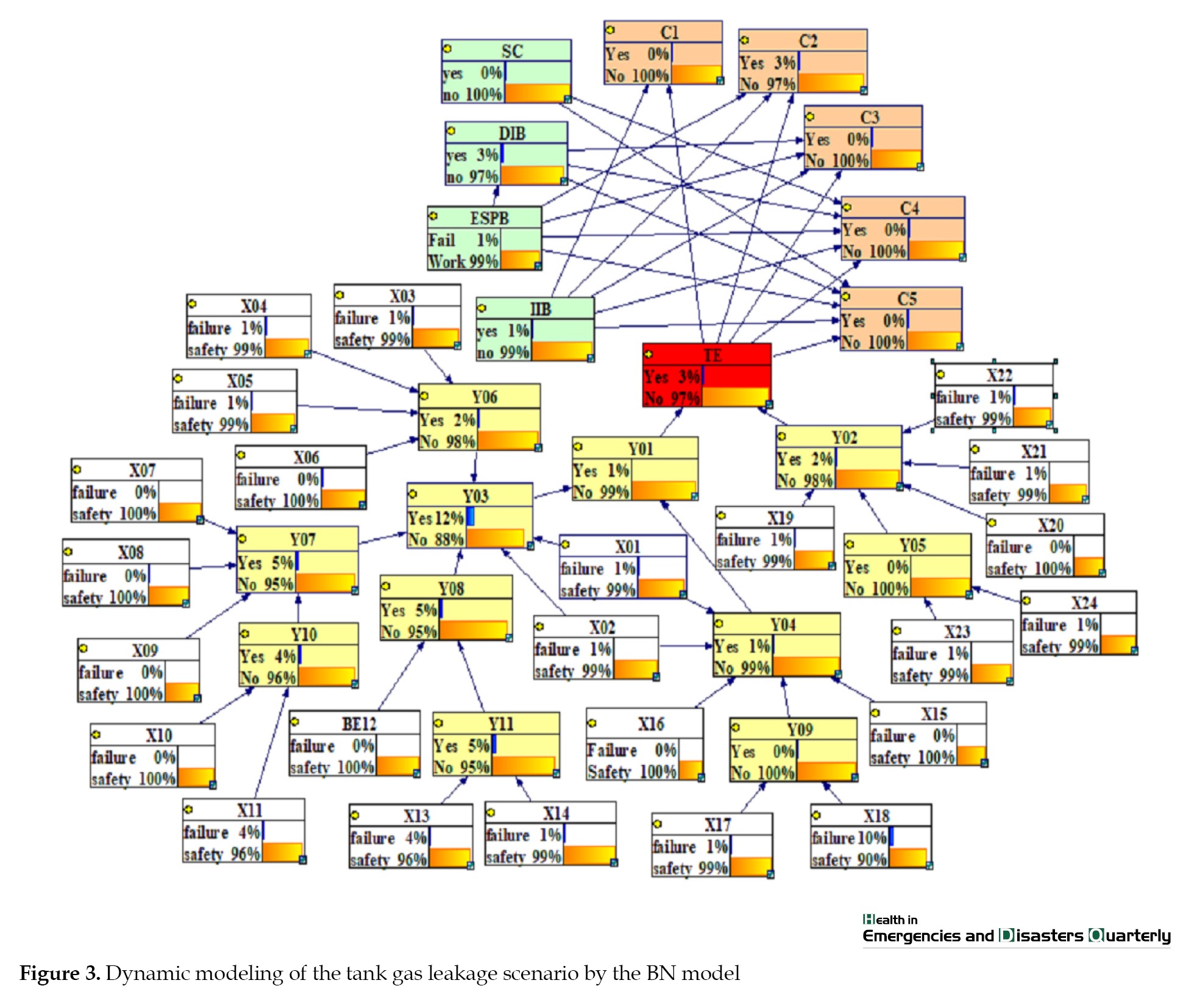
Figure 3 displays a BN model of the tank gas leakage scenario. The probability values for essential events, safety barriers, and intermediate events, as determined through fuzzy logic, were integrated into the model. Subsequently, the developed FBN served as the foundation for deriving the probability values of intermediate events, the top event, and its associated consequences (Tables 6 and 7).
To update the presented model, the central node representing the tank gas leak was designated as evidence, and the prior probabilities of all basic events, intermediate events, and consequences were accordingly updated. The outcomes of this model revision are presented in the fourth column of Tables 6 and 7.
Sensitivity analysis
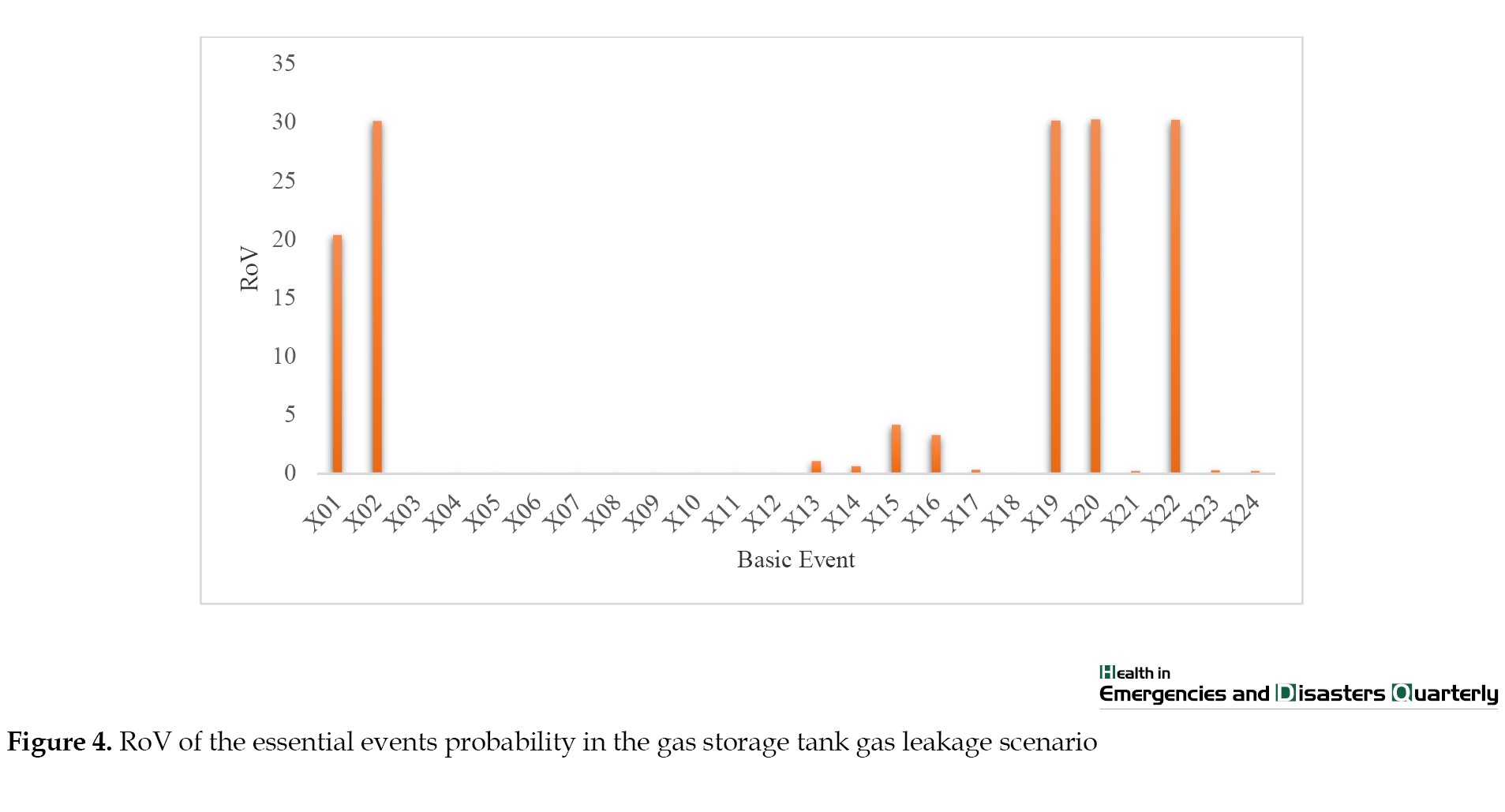
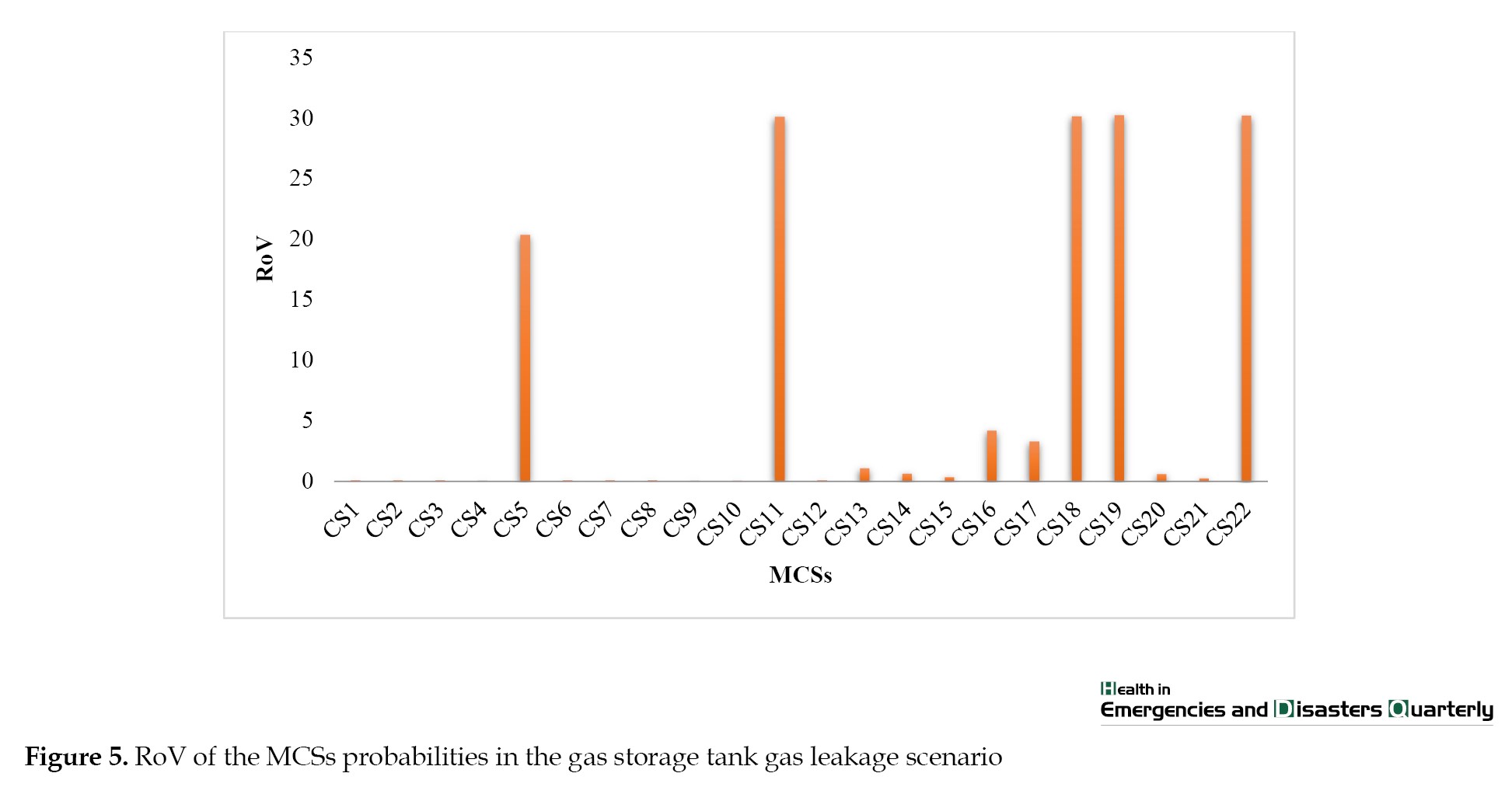
As shown in Figure 4, X20 (inappropriate installation), X19 (inappropriate connections), and X02 (pressure safety valve [PSV] failure) have the highest RoV of probability, indicating that the occurrence of the top event (gas storage tank gas leak) is most strongly influenced by the critical essential events. Figure 5 shows the results of ranking the gas storage tank scenario for MCSs according to the RoV. As illustrated, CS19, CS18, and CS11 are determined to be the most critical MCSs.
Discussion
The primary objective of this research is to solve the problems of insufficient reliable and accurate data, staticity, and incompatibility with dynamic accidents in risk assessment studies. For this purpose, a functional framework based on fuzzy logic and the BN was presented to resolve the challenges.
Among the risk analysis techniques for accidents, the BT model has been widely validated as an effective and dependable approach [16]. The model has been commonly used in various safety and risk analysis fields, including process safety analysis, accident risk assessment, risk management, and the implementation of safety barriers [38, 39]. According to the results obtained by implementing this model in the investigated scenario, it was determined that 24 essential events and 11 intermediate events are responsible for the gas storage tank gas leakage. The present study recognized immediate and delayed ignition systems, emergency stop push buttons, and space confinement as safety barriers safeguarding against gas storage tank gas leakage.
BT method provides a strong model for delineating the initial causes that precipitate the main event (scenario) occurrence and for predicting the ultimate consequences of the scenario’s realization [40]. However, one of the shortcomings of the BT methodology is the use of general defective data in databases, which consequently results in uncertainty within the results, attributable to the lack of specificity and the outdated nature of the data about the studied unit [13, 41]. To overcome this limitation, fuzzy logic was used to calculate the probability of the occurrence of basic events and reduce uncertainty in the results.
Jozi et al., Solanzadeh et al., and Mirzaei Aliabadi reported the problem of insufficient data on defects and lack of certainty in the process industry in their studies [2, 25, 42]. The existence of these problems justifies the use of fuzzy logic. Applying fuzzy logic in the FTA and the ETA can simplify the assessment and increase the accuracy [43-45]. Recent studies show that the accuracy of predicting the probability of fundamental event failures using fuzzy numbers from different experts can vary in diverse environments. Accurately selecting the fuzzy number to represent the basic event is crucial. This approach ultimately decreases uncertainty and enhances the system’s reliability [46]. Fuzzy logic represents the parameters of a problem (occurrence rate of essential events, the top event of an accident scenario, etc.) as fuzzy numbers in a range instead of limiting them to a number. In this sense, fuzzy logic offers a precise and systematic framework for representing and reasoning about complex, uncertain phenomena in reality [27, 47]. Additional significant constraints of the BT methodology include its static nature and inability to accommodate dynamic accident scenarios. This condition has evolved into a critical concern within the field of quantitative risk assessment in process industries [1, 16]. Although fuzzy theory can reduce uncertainty, it can not perform deductive reasoning (probability update) in the structure of fuzzy methods, such as fuzzy fault tree, fuzzy BT mode, and so on [35]. In this study, the BN logic was used to overcome this problem. The BN was also used in dynamic quantitative risk analysis. In the BN, after receiving new information such as pseudo-accident statistics, accidents, etc. the probability of basic events is updated; in other words, safety analysis turns into a dynamic mode [18, 20]. In their studies, Wu et al., Rezaee et al., and Zhang et al. showed the significance of employing the FBN in dynamic assessment and control of process industries to overcome the problems of conventional risk analysis methods and reduce their uncertainty [48-50]. The BN model allows for inductive reasoning, which estimates the probability of a scenario’s realization and consequences [51]. Inductive reasoning using the BN method indicates that the gas leakage from gas storage tank most likely results in the top event occurring with a probability of 3.19×10-2. The subsequent consequences, a near miss and a high material release have probabilities of 3.14×10-2 and 2.82×10-4, respectively. Unlike traditional risk analysis methods like BT, the BN method accounts for the conditional dependence between events of defect type and common causes [52]. This is illustrated in Figure 3 by the dependency between Y02 and Y03, which share common causes X01 and X02.
The BN’s deductive inference capability is crucial for dynamic risk analysis. Deductive inference enables the revision of basic event probabilities, thereby reducing uncertainty within the model and its resulting outputs [53, 54]. Revising the probabilities of essential events and their corresponding consequences can identify the most critical (most influential) essential events that significantly impact the occurrence of the top event [17].
The revised probability of each basic event (Xi) is determined by assuming the probability of basic event (Xi) occurrence given the top event (gas storage tank gas leakage), represented as P(Xi | gas storage tank gas leakage). In this investigation, X21 (inappropriate filtering) was determined to be the most influential factor in the occurrence of the analyzed scenario. Furthermore, after updating the probability of the top event, C2 remains the most likely consequence. This is primarily attributed to the effective functioning of the emergency stop push button during gas leaks from the storage tank. C1 (jet fire), with a probability of 8.76×10-4, is the second most probable consequence due to the potential for immediate ignition in the surrounding area. Consequently, implementing barriers in the gas storage tank system can substantially mitigate the impacts of gas leaks.
The FBN, a fusion of fuzzy theory and BNs, leverages fuzzy numbers to represent basic event probabilities and safety barrier effectiveness, thereby mitigating uncertainty [34, 35]. Moreover, it benefits from both deductive and inductive inference. Consequently, the BN emerges as a robust and efficient tool for addressing uncertainty in risk analysis studies [27].
Wang et al. concluded that the use of updated values for the probability of essential events as well as the final consequences for determining the identification of the most influential essential events and probable outcomes could lead to errors in selecting these elements. They used the RoV of probabilities to solve this problem [37]. In the present study, based on Figure 4 (RoV of the essential events), X20 (inappropriate installation), X19 (inappropriate connections), and X02 (PSV failure) were determined to be the most influential essential events in the realization of the top event. Moreover, Figure 5 shows that the most influential MCSs variables coincide with the basic events identified as the most critical in Figure 4.
Conclusion
The present study offers a thorough and dynamic quantitative risk analysis of explosion and fire hazards in process industries, utilizing a combination of fuzzy logic and BNs. The gas storage tank system was selected as a study unit, considering the history of previous accidents and its critical role in the normal operation of the process. Therefore, the probabilistic risk analysis considered gas leakage from the gas storage tank (the main scenario) and its fire and explosion. The analysis of the scenario’s cause-consequence was performed using the BT diagram, basic events, intermediate events, safety barriers, and identification of the probable consequences of gas leakage from a gas storage tank. The fuzzy logic technique was used to determine the probability of basic events in the BT model and reduce their uncertainty probability. To refine the probability analysis and uncover the interdependencies among the contributing factors to the critical event, the BN was employed to represent the fault tree diagram. This analysis determined that inappropriate installation and near-miss incidents were the primary causes and consequences of gas storage tank gas leakage. The RoV analysis identifies the most influential basic events in the top event occurrence with high sensitivity.
Ethical Considerations
Compliance with ethical guidelines
This study was approved by the Ethics Committee of the Hamadan University of Medical Sciences, Hamadan, Iran (Code: 9512037370).
Funding
This research was extracted from the master’s thesis of Tahereh Eskandari, approved by the Department of Occupational Health, School of Public Health, Hamadan University of Medical Sciences, Hamadan, Iran. The study was supported by Hamadan University of Medical Sciences, Hamadan, Iran, and the National Oil Products Distribution Company in Hamadan City, Iran.
Authors' contributions
All authors equally contributed to preparing this article.
Conflict of interest
The author(s) declared no conflict of interest regarding this article’s research, authorship, or publication.
Acknowledgments
The authors would like to acknowledge the valuable contributions of Hamadan University of Medical Sciences, Hamadan, Iran, and the National Oil Products Distribution Company in Hamadan City, Iran.
References
Process industries, characterized by high equipment density, hazardous materials, a large workforce, process complexity, and significant potential for accidents and catastrophic consequences, are classified as complex systems [1]. In the process industries, human factors have been identified as one of the most common causes of catastrophic accidents [2]. The reason for this conclusion can be the large number of employees in these industries [1, 2]. Additionally, the substantial quantities of flammable hydrocarbons typically stored in these industries amplify the risk of catastrophic events with far-reaching consequences: Financial, life-threatening, and environmental [2, 3]. In the meantime, fires and explosions can cause significant damage [4, 5]. In the recent fire and explosion catastrophic accidents in Texas Refinery in March 2005, 15 people were killed, 180 people were injured, and a financial loss of 1.5 billion USD was left [6]. In the horrible explosion in Toronto Propane storage facilities in 2008, 2 people were killed, and thousands of people were evacuated. Moreover, in the horrible fire and explosion in the British Petroleum Deepwater Horizon sea platform due to oil leakage in 2010, 11 people were killed, and financial and environmental losses of 36.9 billion USD were made [6].
These accidents prompted safety experts to prioritize upgrading safety systems and conducting risk-based studies to implement appropriate control measures. Given the significant losses resulting from numerous fire and explosion accidents in process industries, establishing a decision-making standard and prioritizing hazards has become necessary. Consequently, decision-making and management now rely on risk assessment [2, 7].
Risk analysis serves as a crucial tool for formulating accident prevention strategies and practical risk mitigation measures within complex systems. Simultaneously, its primary objective is to yield actionable insights to inform accident prevention efforts or mitigate the severity of accident consequences [8].
Various methods are employed to identify and evaluate risks. The choice of an appropriate approach hinges on factors such as available data, industry context, desired outcomes, financial limitations, and time constraints [9]. In process industries, traditional risk assessment methods include fault tree analysis (FTA), event tree analysis (ETA), and bowtie technique [10-12]. These approaches depend on imperfect, non-specific data, which can introduce uncertainty into the results due to their lack of relevance to the specific plant under study and its outdated nature [13]. Consequently, discovering a technique to minimize the uncertainty associated with the prior failure rate of fundamental events holds great importance. Fuzzy logic is suggested to reduce uncertainty in estimating the probability of basic event occurrences. Numerous studies have demonstrated that the fuzzy approach can be instrumental when dealing with events lacking sufficient data for calculating occurrence probabilities in their databases [14, 15]. Traditional risk assessment methods often grapple with the challenge of staticity. Consequently, they struggle to effectively analyze the risks associated with dynamic systems [16-18]. In process industries, the Bayesian network (BN) serves as an excellent tool for conducting quantitative analyses [17]. A BN provides a probabilistic approach to handling uncertainty and can mitigate the limitations of traditional methods. It considers conditional dependencies, common defects, and various modes of basic events during the risk assessment process. One of the key benefits of BNs lies in their capacity to update probabilities, making it an excellent approach for assessing risk in dynamic systems [19, 20].
The primary objective of this study is to conduct an explosion risk analysis of a tank employed in an industrial process. This study uses a combination of tools: The bowtie diagram is used for analyzing the causes and consequences of a specific scenario, an approach using fuzzy logic to assess the likelihood of essential events, and BNs are used to discern the nature and patterns of connections among the contributing factors behind catastrophic events.
Materials and Methods
The current cross-sectional study investigated the process industry. The gas storage tank under study was chosen due to its historical records of past events and crucial role in maintaining normal process operations. This study conducted a probabilistic risk assessment of gas storage tank, gas leakage, fire, and explosion using the Bayesian tree (BT) model and Fuzzy-BN (FBN). The study steps were as follows.
Bowtie technique
The bowtie analysis is a graphical method that illustrates the complete sequence of events leading to an accident. It begins by identifying the causes of the accident and traces them through to their potential consequences. BT combines FTA and ETA to provide a comprehensive view of the risk [21, 22].
Investigating the primary factors behind the chosen scenario (the top event) involved applying the FTA method. This structured and hierarchical method illustrates how an undesirable accident can arise by linking intermediate and basic events. In FTA, the undesired accident is typically identified as the top event. This approach illustrates the relationships between events and their causes through logical ‘AND’ and ‘OR’ gateways [23, 24]. The ETA approach was employed to assess potential consequences that might arise in the event of a top-event incident and the failure of each safety barrier. At each stage of the event tree, the final implications due to the occurrence of the top event are determined by creating two branches of success and failure related to safety [25]. This study employed a combination of direct observation, expert interviews, and document and operational map review.
Fuzzy approach
In most risk analysis studies, the probability of basic events occurring is extracted from the defect rate of the events databases. This information may not be up-to-date on the desired event. Also, the defect rate of the desired event is often not accurately found, and similar event data should be used. This condition causes considerable uncertainty in data and results [26, 27]. In this research, fuzzy logic is applied to mitigate the uncertainty associated with the probability of essential events occurring in the developed FTA model. There are five steps for calculating the probability of failure for each crucial event. These steps begin with selecting a team of experts and end with the probability estimate. Probability estimation is often achieved by applying the trapezoidal and Onisawa formulas.
Step 1: Expert selection
The expert’s opinion is used when there is not enough information. In this study, an expert is someone who has complete information about the system and is familiar with FTA and ETA methods. Five experts were appointed in this study.
Step 2: Weighing the experts
Knowing that the experts have different criteria such as job title, education, years of related experience, etc. a relative weighting factor was determined based on the Likert score scale to apply the probability of basic events occurrence (Table 1).

Referring to Table 1, the relative weighting factor for each expert consists of the sum of the Likert scores gained by each expert divided by the sum of the scores gained by all experts [28, 29].
Step 3: Quantification
Seven language terms and trapezoidal functions (Table 2) were used to quantify experts’ opinions on essential events.

Chen and Hwang’s method was employed to quantify experts’ opinions [30].
Then, experts’ opinions were integrated based on the study conducted by Clemen and Winkler [31] and using fuzzy number theory and Equation 1:
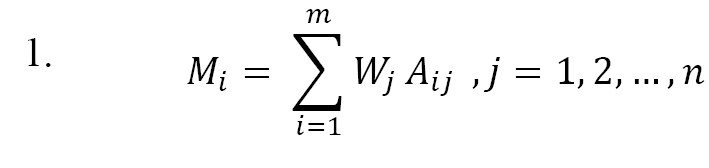
, where Wj is the weight of expert j, Aij is the linguistic term set by the expert j to the event i, j is the number of experts, and Mi is the integrated experts’ opinion (fuzzy probability of basic event i failure).
Step 4: De-fuzzing
In this stage, the obtained numbers, which are equivalent to the experts’ opinion and still in “probable” mode, became de-fuzzy using the Equation of gravitation center (trapezoid) (Equation 2) [32].
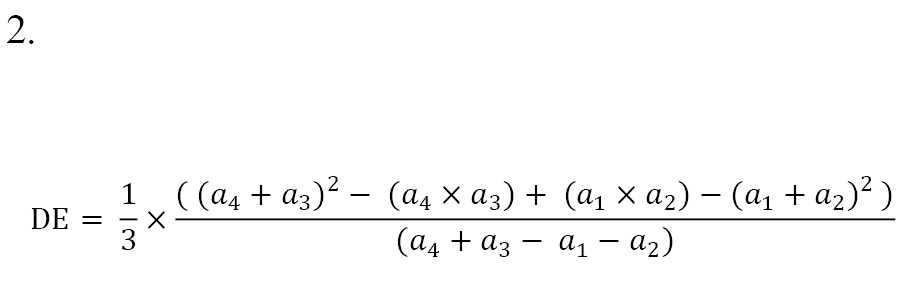
Step 5: Converting probable numbers to probabilities
The numbers obtained from the de-fuzzing step are still in the “probable” mode. Since the fault tree accepts probability, the obtained numbers must be converted from probable to probability. For this purpose, Onisawa formula and Equations 3 and 4 are used [33, 34].
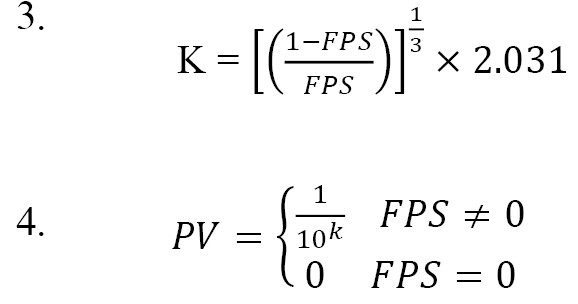
Although fuzzy theory can significantly reduce uncertainty, it cannot perform deductive reasoning (probability update) in the structure of the used fuzzy methods, such as fuzzy FTA and fuzzy BT model [35]. This study used the BN’s logic to overcome this limitation.
BN
After constructing the scenario using the BT model and assessing the probabilities of essential events and safety barriers through fuzzy logic, the resulting model was migrated to the BN framework to address its shortcomings and limitations. The transfer algorithm (mapping) from the BT model to the BN was developed based on research conducted by Khakzad et al [17]. A Bayesian BT model was developed and analyzed using GeNIe software for this study. Figure 1 illustrates the algorithm for transferring data BT to the BN. The basic events, intermediate events, central events, safety barriers, and consequences in the BT model are respectively mapped to root nodes, intermediate nodes, central nodes, safety barrier nodes, and consequence nodes in the BN model.
To quantify the model, fuzzy probabilities of essential events were used as root node probabilities. In BN models, conditional probability distribution tables are employed to estimate the probability of intermediate events. The probability of an intermediate node is calculated based on the conditional dependencies between the root nodes and the probabilistic conditional relations for all possible states of the node variables. The probability of the central node was determined using the same method. Equation 5 was applied to the BN to calculate the joint probability distribution of the set of variables U = (x1, ..., xn).
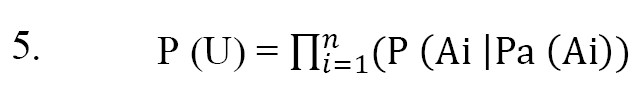
, where Pa (Ai) is the parent set of Ai in BN, and P (U) represents the properties of the BN [17, 36].
The most effective basic events were identified after creating a qualitative and quantitative model for the selected scenario using probability update features (nodes and consequences) and conducting a sensitivity analysis. In diagnostic analysis, BNs employ Bayes’ theorem to update prior probabilities based on new observations from a distinct set of variables known as evidence (often denoted as ‘E’). The probability distribution can be computed using various inference algorithms, including connection tree and variable elimination, grounded in Bayes’ theorem (Equation 6).
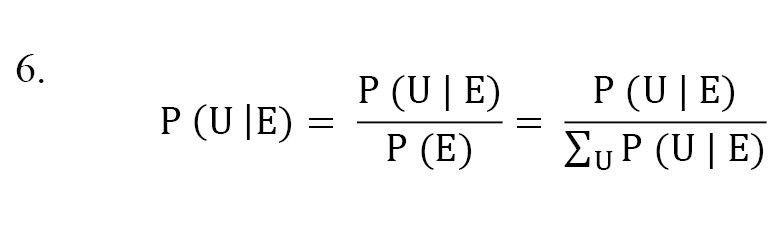
Sensitivity analysis
Sensitivity analysis was done using the rate of variation (RoV) approach.
RoV approach
The rate of variation is used to select the most effective essential events and minimal cut sets (MCSs) [37]. The RoV value is determined by Equations 7 and 8.
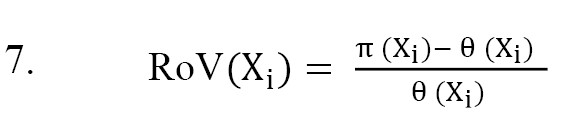
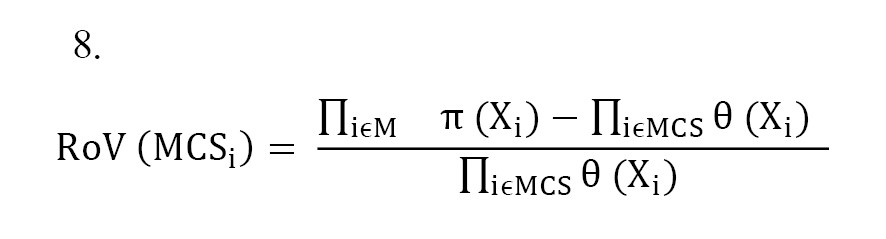
, where, π (Xi) and θ (Xi) represent the posterior and prior probabilities of the Xi essential event, respectively, and and represent posterior and prior probabilities, respectively.
Results
Drawing the BT diagram
The BT diagram of the gas storage tank gas leakage scenario is presented in Figure 2, where the FTA is located on the left side, and the ETA is on the right. The fault tree associated with the gas storage tank gas leak (top event) indicates that tank performance and plumbing system failure were identified as the main intermediate causes. These causes were categorized as intermediate and basic events. The symbols, descriptions, and probabilities of the basic events are presented in Table 3.

The event tree section was drawn considering four safety barriers: Immediate ignition barrier, emergency stop pushes button, delay ignition barrier, and space confinement, to sequence the events after the top event occurrence. The first and second columns of Table 4 show the symbols, descriptions, and defect probabilities of safety barriers.

Considering the performance of the safety barriers, either failure or proper and expected operation, the gas storage tank leakage scenario led to five ultimate consequences, including flash fire, jet fire, vapor cloud explosion, release of materials, and near miss.
The probability of delayed ignition rises with the expansion of the gas vapor cloud and, consequently, the volume of the released gas. Given that the emergency stop push button (ESPB) failure typically results in a larger gas release, the probability of delayed ignition is correspondingly higher (Table 4).
Calculating fuzzy probabilities for basic events and safety barriers
At the outset, a panel of five qualified experts, a chief engineer, a manager, a process engineer, an operational technician, and an operator, was chosen to assess the probability of basic event occurrences. Based on the established criteria for scoring the weight of experts, as outlined in Table 1, the weight of each expert involved in the study was determined, and the results are presented in Table 5.

The linguistic terms in Table 2 were used to gather expert opinions on the probability of essential events and safety barriers failing to prevent the scenario. Moreover, the experts’ views were integrated using Equation 1, and then the experts’ opinions were subjected to a de-fuzzy operation. The fuzzy probability score calculated the number obtained by de-fuzzing each basic event. Finally, the probabilistic numbers (de-fuzzing) were converted into probability values by Equations 3 and 4. The calculation was applied to all 24 basic events, resulting in the identification of the tank gas leak scenario and the safety barriers relevant to preventing its occurrence. Finally, the fuzzy logic approach was used to determine the probability of failure for each basic event. The fuzzy logic outcomes are presented in the third column of Tables 6 and 7.


BN
Figure 3 displays a BN model of the tank gas leakage scenario. The probability values for essential events, safety barriers, and intermediate events, as determined through fuzzy logic, were integrated into the model. Subsequently, the developed FBN served as the foundation for deriving the probability values of intermediate events, the top event, and its associated consequences (Tables 6 and 7).
To update the presented model, the central node representing the tank gas leak was designated as evidence, and the prior probabilities of all basic events, intermediate events, and consequences were accordingly updated. The outcomes of this model revision are presented in the fourth column of Tables 6 and 7.
Sensitivity analysis
As shown in Figure 4, X20 (inappropriate installation), X19 (inappropriate connections), and X02 (pressure safety valve [PSV] failure) have the highest RoV of probability, indicating that the occurrence of the top event (gas storage tank gas leak) is most strongly influenced by the critical essential events. Figure 5 shows the results of ranking the gas storage tank scenario for MCSs according to the RoV. As illustrated, CS19, CS18, and CS11 are determined to be the most critical MCSs.
Discussion
The primary objective of this research is to solve the problems of insufficient reliable and accurate data, staticity, and incompatibility with dynamic accidents in risk assessment studies. For this purpose, a functional framework based on fuzzy logic and the BN was presented to resolve the challenges.
Among the risk analysis techniques for accidents, the BT model has been widely validated as an effective and dependable approach [16]. The model has been commonly used in various safety and risk analysis fields, including process safety analysis, accident risk assessment, risk management, and the implementation of safety barriers [38, 39]. According to the results obtained by implementing this model in the investigated scenario, it was determined that 24 essential events and 11 intermediate events are responsible for the gas storage tank gas leakage. The present study recognized immediate and delayed ignition systems, emergency stop push buttons, and space confinement as safety barriers safeguarding against gas storage tank gas leakage.
BT method provides a strong model for delineating the initial causes that precipitate the main event (scenario) occurrence and for predicting the ultimate consequences of the scenario’s realization [40]. However, one of the shortcomings of the BT methodology is the use of general defective data in databases, which consequently results in uncertainty within the results, attributable to the lack of specificity and the outdated nature of the data about the studied unit [13, 41]. To overcome this limitation, fuzzy logic was used to calculate the probability of the occurrence of basic events and reduce uncertainty in the results.
Jozi et al., Solanzadeh et al., and Mirzaei Aliabadi reported the problem of insufficient data on defects and lack of certainty in the process industry in their studies [2, 25, 42]. The existence of these problems justifies the use of fuzzy logic. Applying fuzzy logic in the FTA and the ETA can simplify the assessment and increase the accuracy [43-45]. Recent studies show that the accuracy of predicting the probability of fundamental event failures using fuzzy numbers from different experts can vary in diverse environments. Accurately selecting the fuzzy number to represent the basic event is crucial. This approach ultimately decreases uncertainty and enhances the system’s reliability [46]. Fuzzy logic represents the parameters of a problem (occurrence rate of essential events, the top event of an accident scenario, etc.) as fuzzy numbers in a range instead of limiting them to a number. In this sense, fuzzy logic offers a precise and systematic framework for representing and reasoning about complex, uncertain phenomena in reality [27, 47]. Additional significant constraints of the BT methodology include its static nature and inability to accommodate dynamic accident scenarios. This condition has evolved into a critical concern within the field of quantitative risk assessment in process industries [1, 16]. Although fuzzy theory can reduce uncertainty, it can not perform deductive reasoning (probability update) in the structure of fuzzy methods, such as fuzzy fault tree, fuzzy BT mode, and so on [35]. In this study, the BN logic was used to overcome this problem. The BN was also used in dynamic quantitative risk analysis. In the BN, after receiving new information such as pseudo-accident statistics, accidents, etc. the probability of basic events is updated; in other words, safety analysis turns into a dynamic mode [18, 20]. In their studies, Wu et al., Rezaee et al., and Zhang et al. showed the significance of employing the FBN in dynamic assessment and control of process industries to overcome the problems of conventional risk analysis methods and reduce their uncertainty [48-50]. The BN model allows for inductive reasoning, which estimates the probability of a scenario’s realization and consequences [51]. Inductive reasoning using the BN method indicates that the gas leakage from gas storage tank most likely results in the top event occurring with a probability of 3.19×10-2. The subsequent consequences, a near miss and a high material release have probabilities of 3.14×10-2 and 2.82×10-4, respectively. Unlike traditional risk analysis methods like BT, the BN method accounts for the conditional dependence between events of defect type and common causes [52]. This is illustrated in Figure 3 by the dependency between Y02 and Y03, which share common causes X01 and X02.
The BN’s deductive inference capability is crucial for dynamic risk analysis. Deductive inference enables the revision of basic event probabilities, thereby reducing uncertainty within the model and its resulting outputs [53, 54]. Revising the probabilities of essential events and their corresponding consequences can identify the most critical (most influential) essential events that significantly impact the occurrence of the top event [17].
The revised probability of each basic event (Xi) is determined by assuming the probability of basic event (Xi) occurrence given the top event (gas storage tank gas leakage), represented as P(Xi | gas storage tank gas leakage). In this investigation, X21 (inappropriate filtering) was determined to be the most influential factor in the occurrence of the analyzed scenario. Furthermore, after updating the probability of the top event, C2 remains the most likely consequence. This is primarily attributed to the effective functioning of the emergency stop push button during gas leaks from the storage tank. C1 (jet fire), with a probability of 8.76×10-4, is the second most probable consequence due to the potential for immediate ignition in the surrounding area. Consequently, implementing barriers in the gas storage tank system can substantially mitigate the impacts of gas leaks.
The FBN, a fusion of fuzzy theory and BNs, leverages fuzzy numbers to represent basic event probabilities and safety barrier effectiveness, thereby mitigating uncertainty [34, 35]. Moreover, it benefits from both deductive and inductive inference. Consequently, the BN emerges as a robust and efficient tool for addressing uncertainty in risk analysis studies [27].
Wang et al. concluded that the use of updated values for the probability of essential events as well as the final consequences for determining the identification of the most influential essential events and probable outcomes could lead to errors in selecting these elements. They used the RoV of probabilities to solve this problem [37]. In the present study, based on Figure 4 (RoV of the essential events), X20 (inappropriate installation), X19 (inappropriate connections), and X02 (PSV failure) were determined to be the most influential essential events in the realization of the top event. Moreover, Figure 5 shows that the most influential MCSs variables coincide with the basic events identified as the most critical in Figure 4.
Conclusion
The present study offers a thorough and dynamic quantitative risk analysis of explosion and fire hazards in process industries, utilizing a combination of fuzzy logic and BNs. The gas storage tank system was selected as a study unit, considering the history of previous accidents and its critical role in the normal operation of the process. Therefore, the probabilistic risk analysis considered gas leakage from the gas storage tank (the main scenario) and its fire and explosion. The analysis of the scenario’s cause-consequence was performed using the BT diagram, basic events, intermediate events, safety barriers, and identification of the probable consequences of gas leakage from a gas storage tank. The fuzzy logic technique was used to determine the probability of basic events in the BT model and reduce their uncertainty probability. To refine the probability analysis and uncover the interdependencies among the contributing factors to the critical event, the BN was employed to represent the fault tree diagram. This analysis determined that inappropriate installation and near-miss incidents were the primary causes and consequences of gas storage tank gas leakage. The RoV analysis identifies the most influential basic events in the top event occurrence with high sensitivity.
Ethical Considerations
Compliance with ethical guidelines
This study was approved by the Ethics Committee of the Hamadan University of Medical Sciences, Hamadan, Iran (Code: 9512037370).
Funding
This research was extracted from the master’s thesis of Tahereh Eskandari, approved by the Department of Occupational Health, School of Public Health, Hamadan University of Medical Sciences, Hamadan, Iran. The study was supported by Hamadan University of Medical Sciences, Hamadan, Iran, and the National Oil Products Distribution Company in Hamadan City, Iran.
Authors' contributions
All authors equally contributed to preparing this article.
Conflict of interest
The author(s) declared no conflict of interest regarding this article’s research, authorship, or publication.
Acknowledgments
The authors would like to acknowledge the valuable contributions of Hamadan University of Medical Sciences, Hamadan, Iran, and the National Oil Products Distribution Company in Hamadan City, Iran.
References
- Azadeh A, Fam IM, Azadeh MA. Integrated HSEE management systems for industry: A case study in gas refinary. Journal of the Chinese Institute of Engineers. 2009; 32(2):235-41. [Link]
- Soltanzadeh A, Mohammadfam I, Moghimbeigi A, Ghiasvand R. Key factors contributing to accident severity rate in construction industry in Iran: A regression modelling approach. Arhiv za Higijenu Rada i Toksikologiju. 2016; 67(1):47-53. [DOI:10.1515/aiht-2016-67-2687] [PMID]
- Mohammadfam I, Zarei E, Yazdi M, Gholamizadeh K. Quantitative risk analysis on rail transportation of hazardous materials. Mathematical Problems in Engineering. 2022; 2022(1):6162829. [DOI:10.1155/2022/6162829]
- Borgheipour H, Tehrani GM, Eskandari T, Mohammadieh OC, Mohammadfam I. Dynamic risk analysis of hydrogen gas leakage using Bowtie technique and Bayesian network. International Journal of Environmental Science and Technology. 2021; 18:3613–24. [Link]
- Mohammadfam I, Khajevandi AA, Dehghani H, Babamiri M, Farhadian M. Analysis of factors affecting human reliability in the mining process design using Fuzzy Delphi and DEMATEL methods. Sustainability. 2022 ; 14(13):8168. [DOI:10.3390/su14138168]
- Smith LC, Smith M, Ashcroft P. Analysis of environmental and economic damages from British Petroleum’s Deepwater Horizon oil spill. Albany Law Review. 2011; 74(1):563-85. [DOI:10.2139/ssrn.1653078]
- Zhu Y, Qian XM, Liu ZY, Huang P, Yuan MQ. Analysis and assessment of the Qingdao crude oil vapor explosion accident: Lessons learnt. Journal of Loss Prevention in the Process Industries. 2015; 33:289-303. [DOI:10.1016/j.jlp.2015.01.004]
- Gerba CP. Risk assessment. In: Brusseau ML, Pepper IL, Gerba CP, editors. Environmental and pollution science. Academic Press: Massachusetts; 2019. [DOI:10.1016/B978-0-12-814719-1.00029-X]
- Azadeh A, Fam M, Garakani MM. A total ergonomic design approach to enhance the productivity in a complicated control system. Information Technology Journal. 2007; 6(7):1036-42. [DOI:10.3923/itj.2007.1036.1042]
- Analouei R, Taheriyoun M, Safavi HR. Risk assessment of an industrial wastewater treatment and reclamation plant using the bowtie method. Environmental Monitoring and Assessment. 2020; 192(1):33. [DOI:10.1007/s10661-019-7995-x] [PMID]
- Hosseini N, Givehchi S, Maknoon R. Cost-based fire risk assessment in natural gas industry by means of fuzzy FTA and ETA. Journal of Loss Prevention in the Process Industries. 2019; 63:104025. [DOI:10.1016/j.jlp.2019.104025]
- Seker S. Analyzing occupational risks of pharmaceutical industry under uncertainty using a Bowtie analysis. An International Journal of Optimization and Control: Theories & Applications (IJOCTA). 2019; 9(2):113-24. [DOI:10.11121/ijocta.01.2019.00655]
- Li X, Chen G, Zhu H. Quantitative risk analysis on leakage failure of submarine oil and gas pipelines using Bayesian network. Process Safety and Environmental Protection. 2016; 103:163-73. [DOI:10.1016/j.psep.2016.06.006]
- Arunraj N, Mandal S, Maiti J. Modeling uncertainty in risk assessment: An integrated approach with fuzzy set theory and Monte Carlo simulation. Accident Analysis & Prevention. 2013; 55:242-55. [DOI:10.1016/j.aap.2013.03.007] [PMID]
- Sa’idi E, Anvaripour B, Jaderi F, Nabhani N. Fuzzy risk modeling of process operations in the oil and gas refineries. Journal of Loss Prevention in the Process Industries. 2014; 30:63-73. [DOI:10.1016/j.jlp.2014.04.002]
- Abimbola M, Khan F, Khakzad N. Dynamic safety risk analysis of offshore drilling. Journal of Loss Prevention in the Process Industries. 2014; 30:74-85. [DOI:10.1016/j.jlp.2014.05.002]
- Khakzad N, Khan F, Amyotte P. Dynamic safety analysis of process systems by mapping bowtie into Bayesian network. Process Safety and Environmental Protection. 2013; 91(1-2):46-53. [DOI:10.1016/j.psep.2012.01.005]
- Yang X, Mannan MS. The development and application of dynamic operational risk assessment in oil/gas and chemical process industry. Reliability Engineering & System Safety. 2010; 95(7):806-15. [DOI:10.1016/j.ress.2010.03.002]
- Mohammadfam I, Ghasemi F, Kalatpour O, Moghimbeigi A. Constructing a Bayesian network model for improving safety behavior of employees at workplaces. Applied Ergonomics. 2017; 58:35-47. [DOI:10.1016/j.apergo.2016.05.006] [PMID]
- Zhang G, Thai VV, Yuen KF, Loh HS, Zhou Q. Addressing the epistemic uncertainty in maritime accidents modelling using Bayesian network with interval probabilities. Safety Science. 2018; 102:211-25. [DOI:10.1016/j.ssci.2017.10.016]
- Harris J, Everingham J, Barclay MA, Kirsch P, Cliff D. The application of bow-tie analysis to the well-being of fly-in, fly-out mining, oil and gas workers. Paper presented at: Minesafe International Conference. 1-2 May 2017; Perth, WA, Australia.[Link]
- van Staalduinen MA, Khan F, Gadag V, Reniers G. Functional quantitative security risk analysis (QSRA) to assist in protecting critical process infrastructure. Reliability Engineering & System Safety. 2017; 157:23-34. [DOI:10.1016/j.ress.2016.08.014]
- Cai B, Liu Y, Zhang Y, Fan Q, Liu Z, Tian X. A dynamic Bayesian networks modeling of human factors on offshore blowouts. Journal of Loss Prevention in the Process Industries. 2013; 26(4):639-49. [DOI:10.1016/j.jlp.2013.01.001]
- Zulqarnain M, Tyagi M. Quantification of risks associated with a representative production well in the Gulf of Mexico. Paper presented at: ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering. May 31–June 5, 2015; Newfoundland, Canada. [DOI:10.1115/OMAE2015-42115]
- Mirzaei Aliabadi M, Mohammad Fam I, Kalatpour O, Babayi Mesdaraghi Y. [Risk assessment of liquefied petroleum gas (LPG) storage tanks in the process industries using the Bowtie technique (Persian)]. Journal of Occupational Hygiene Engineering. 2016; 3(2):1-11. [DOI:10.21859/johe-03021]
- Ren J, Jenkinson I, Wang J, Xu D, Yang J. An offshore risk analysis method using fuzzy Bayesian network. Journal of Offshore Mechanics and Arctic Engineering. 2009; 131(4):041101. [DOI:10.1115/1.3124123]
- Zhang L, Wu X, Qin Y, Skibniewski MJ, Liu W. Towards a fuzzy Bayesian network based approach for safety risk analysis of tunnel-induced pipeline damage. Risk Analysis. 2016; 36(2):278-301. [DOI:10.1111/risa.12448] [PMID]
- Rajakarunakaran S, Kumar AM, Prabhu VA. Applications of fuzzy faulty tree analysis and expert elicitation for evaluation of risks in LPG refuelling station. Journal of Loss Prevention in the Process Industries. 2015; 33:109-23. [DOI:10.1016/j.jlp.2014.11.016]
- Renjith V, Madhu G, Nayagam VLG, Bhasi A. Two-dimensional fuzzy fault tree analysis for chlorine release from a chlor-alkali industry using expert elicitation. Journal of Hazardous Materials. 2010; 183(1-3):103-10. [DOI:10.1016/j.jhazmat.2010.06.116] [PMID]
- Chen SJ, Hwang CL. Fuzzy multiple attribute decision making methods. In: Fuzzy multiple attribute decision making. lecture notes in economics and mathematical systems, vol 375. Berlin, Heidelberg: Springer; 1992. [DOI:10.1007/978-3-642-46768-4_5]
- Clemen RT, Winkler RL. Combining probability distributions from experts in risk analysis. Risk Analysis. 1999; 19(2):187-203. [DOI:10.1111/j.1539-6924.1999.tb00399.x]
- Hauge S, Lundteigen MA, Hokstad P, Håbrekke S. Reliability prediction method for safety instrumented systems-pds method handbook, 2010 edition. Trondheim: SINTEF ; 2010. [Link]
- Lavasani SM, Yang Z, Finlay J, Wang J. Fuzzy risk assessment of oil and gas offshore wells. Process Safety and Environmental Protection. 2011; 89(5):277-94. [DOI:10.1016/j.psep.2011.06.006]
- Onisawa T. An approach to human reliability in man-machine systems using error possibility. Fuzzy sets and Systems. 1988; 27(2):87-103. [DOI:10.1016/0165-0114(88)90140-6]
- Ghasem A, Mahmoudzadeh S. [Assesment of economic projects in uncertain conditions (fuzzy approach) (Persian)]. Journal of Economic Research (Tahghighat- E- Eghtesadi). 2011; 45(4):83-108. [Link]
- Abimbola M, Khan F, Khakzad N, Butt S. Safety and risk analysis of managed pressure drilling operation using Bayesian network. Safety Science. 2015; 76:133-44. [DOI:10.1016/j.ssci.2015.01.010]
- Wang W, Shen K, Wang B, Dong C, Khan F, Wang Q. Failure probability analysis of the urban buried gas pipelines using Bayesian networks. Process Safety and Environmental Protection. 2017; 111:678-86. [DOI:10.1016/j.psep.2017.08.040]
- Khan FI, Abbasi S. Techniques and methodologies for risk analysis in chemical process industries. Journal of Loss Prevention in the Process Industries. 1998; 11(4):261-77. [DOI:10.1016/S0950-4230(97)00051-X]
- Lauridsen K, Kozine I, Markert F, Amendola A, Christou M, Fiori M. Assessment of uncertainties in risk analysis of chemical establishments. The Assurance project. Final summary report. Roskilde: Risø National Laboratory; 2002. [Link]
- Shahriar A, Sadiq R, Tesfamariam S. Risk analysis for oil & gas pipelines: A sustainability assessment approach using fuzzy based bowtie analysis. Journal of Loss Prevention in the Process Industries. 2012; 25(3):505-23. [DOI:10.1016/j.jlp.2011.12.007]
- Badreddine A, Amor NB. A Bayesian approach to construct bow tie diagrams for risk evaluation. Process Safety and Environmental Protection. 2013; 91(3):159-71. [DOI:10.1016/j.psep.2012.03.005]
- Jozi S, Esmat Saatloo S, Javan Z. [Environmental risk assessment of the olefin plant in Arya Sasol petrochemical complex using fault tree analysis method (Persian)]. Iranian Journal of Health and Environment. 2014; 7(3):385-98. [Link]
- Mirza S, Jafari MJ, Omidvari M, Lavasani SMR. [The application of Fuzzy logic to determine the failure probability in Fault Tree Risk Analysis (Persian)]. Irtiqa Imini Pishgiri Masdumiyat (Safety Promotion and Injury Prevention). 2014; 2(2):113-23. [DOI:10.22037/meipm.v2i2.7052]
- Aqlan F, Ali EM. Integrating lean principles and fuzzy bowtie analysis for risk assessment in chemical industry. Journal of Loss Prevention in the Process Industries. 2014; 29:39-48. [DOI:10.1016/j.jlp.2014.01.006]
- Lavasani SM, Ramzali N, Sabzalipour F, Akyuz E. Utilisation of fuzzy fault tree analysis (FFTA) for quantified risk analysis of leakage in abandoned oil and natural-gas wells. Ocean Engineering. 2015; 108:729-37. [DOI:10.1016/j.oceaneng.2015.09.008]
- Tyagi SK, Pandey D, Tyagi R. Fuzzy set theoretic approach to fault tree analysis. International Journal of Engineering, Science and Technology. 2010; 2(5):276-83. [DOI:10.4314/ijest.v2i5.60165]
- Vinnem J, Bye R, Gran B, Kongsvik T, Nyheim O, Okstad E, et al. Risk modelling of maintenance work on major process equipment on offshore petroleum installations. Journal of Loss Prevention in the Process Industries. 2012; 25(2):274-92. [DOI:10.1016/j.jlp.2011.11.001]
- Rezaee MJ, Yousefi S, Valipour M, Dehdar MM. Risk analysis of sequential processes in food industry integrating multi-stage fuzzy cognitive map and process failure mode and effects analysis. Computers & Industrial Engineering. 2018; 123:325-37. [DOI:10.1016/j.cie.2018.07.012]
- Wu J, Zhou R, Xu S, Wu Z. Probabilistic analysis of natural gas pipeline network accident based on Bayesian network. Journal of Loss Prevention in the Process Industries. 2017; 46:126-36. [DOI:10.1016/j.jlp.2017.01.025]
- Zhang Q, Zhou C, Tian YC, Xiong N, Qin Y, Hu B. A fuzzy probability bayesian network approach for dynamic cybersecurity risk assessment in industrial control systems. IEEE Transactions on Industrial Informatics. 2017; 14(6):2497-506. [DOI:10.1109/TII.2017.2768998]
- Barua S, Gao X, Pasman H, Mannan MS. Bayesian network based dynamic operational risk assessment. Journal of Loss Prevention in the Process Industries. 2016; 41:399-410. [DOI:10.1016/j.jlp.2015.11.024]
- Yuan Z, Khakzad N, Khan F, Amyotte P. Risk analysis of dust explosion scenarios using Bayesian networks. Risk Analysis. 2015; 35(2):278-91. [DOI:10.1111/risa.12283] [PMID]
- Mahdinia M, Mohammadfam I, Soltanzadeh A, Aliabadi MM, Aghaei H. A fuzzy Bayesian network DEMATEL model for predicting safety behavior. International Journal of Occupational Safety and Ergonomics. 2023; 29(1):36-43. [DOI:10.1080/10803548.2021.2015741] [PMID]
- Nadkarni S, Shenoy PP. A Bayesian network approach to making inferences in causal maps. European Journal of Operational Research. 2001; 128(3):479-98. [DOI:10.1016/S0377-2217(99)00368-9]
Type of article: Research |
Subject:
Risk assessment
Received: 2024/05/26 | Accepted: 2024/10/20 | Published: 2025/04/1
Received: 2024/05/26 | Accepted: 2024/10/20 | Published: 2025/04/1
Send email to the article author
| Rights and permissions | |
 |
This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License. |